
已知动点P以每秒2cm的速度沿如图所示的边框按从B?C?D?E?F?A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm; CD= cm; DE= cm; EF= cm
(3)求出图乙中的a与b的值.
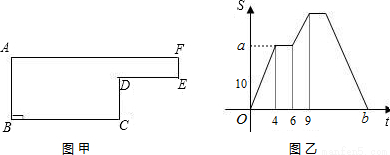
(1) CD和EF;(2) 8cm; 4cm ; 6cm; 2 cm;(3)a=24,b=17
【解析】
试题分析:(1)利用底高相同,面积相等可知点P在CD和EF上△ABP的面积S保持不变;
(2)先根据△ABC的面积为24cm2,AB=6cm,求出BC的长度,再由动点P在BC上运动的时间是4秒,即可求出动点的速度v;由动点P在CD上移动的时间为2秒及速度v,即可求出线段CD的长度,同理,由动点P在DE上移动的时间为3秒及(1)中求出的动点的速度v,即可求出线段DE的长度;
(3)当t=9秒时,动点P移动到点E,则a=S= AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.
AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.
试题解析:(1)根据题意知:点P在CD和EF上△ABP的面积S保持不变;
(2)由图可知,当点P在BC上移动时,△PAB可看作以AB为底、BP为高,则它的面积S随BP的增大而增大,当点P到达点C时面积达到最大值24,
∵S△ABC=24,
∴ ×6×BC=24,
×6×BC=24,
∴BC=8(cm),
又∵点P在BC上移动了4秒,
∴BC=4v,
∴4v=8,
∴v=2(cm/s);
当点P在CD上移动时,底边AB不变,高不变,因而面积不变,恒为24,由图象可知
点P移动的时间为6-4=2(s),
则CD=2×2=4(cm).
当点P在DE上移动时,△PAB可看作以AB为底、BP为高,则它的面积S随BP的增大而增大,当点P到达点E时面积达到最大值a,
∵点P在DE上移动了9-6=3(s),
∴DE=3×2=6(cm);
EF=AB-CD=6-4=2cm.
(3)∵点P移动到点E时面积达到最大值a,
∴a= AB•(BC+DE),
AB•(BC+DE),
∵AB=6cm,BC=8cm,DE=6cm,
∴a= ×6×(8+6)=42(cm2).
×6×(8+6)=42(cm2).
∵FA=BC+DE=8+6=14(cm),CD+EF=AB=6cm,
∴BC+CD+DE+EF+FA=(BC+DE)+(CD+EF)+FA=14+6+14=34(cm),
∴b=34÷2=17 (s).
考点:动点问题的函数图象.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:2015届河南平顶山华英学校八年级下学级第一次月考数学试卷(解析版) 题型:解答题
有人问一位老师,他所教的班有多少学生,老师说:“一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生念外语,还剩下不足6位同学在操场踢足球”.试问这个班共有多少位学生?
查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,正方形的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
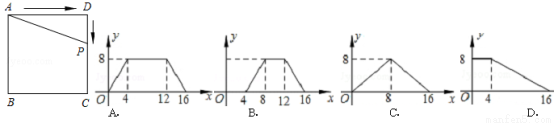
查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市八年级下学期期末考试数学试卷(解析版) 题型:选择题
矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
查看答案和解析>>
科目:初中数学 来源:2015届河北省滦南县八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1 000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
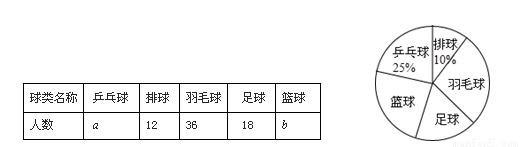
解答下列问题:
(1)本次调查中的样本容量是 ;
(2)求出a与b的值.
(3)试估计上述1 000名学生中最喜欢羽毛球运动的人数.
查看答案和解析>>
科目:初中数学 来源:2015届河北省滦南县八年级下学期期中考试数学试卷(解析版) 题型:填空题
某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在扇形统计图中,“其他”所在扇形的圆心角等于 度;
(2)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 .
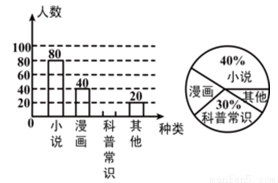
查看答案和解析>>
科目:初中数学 来源:2015届河北省唐山市八年级下学期期末考数学试卷(解析版) 题型:解答题
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF、FD.
(1)求证:四边形AFDC是平行四边形;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.

查看答案和解析>>
科目:初中数学 来源:2015届江西省高安市八年级下学期期末考试数学试卷(解析版) 题型:选择题
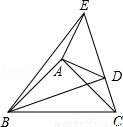
已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;
②BD⊥CE;
③∠ACE+∠DBC=45°;
④BE2=2(AD2+AB2),
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com