
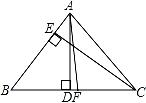
如图,在△ABC中,AD,CE是高线,AF是角平分线,∠BAC=∠AFD=80°.
(1)求∠BCE的度数;
(2)如果AD=6,BE=5.求△ABC的面积.
【考点】三角形内角和定理;三角形的面积;含30度角的直 角三角形.
角三角形.
【分析】(1)先由直角三角形的性质求出∠ADF的度数,再由角平分线的性质求出∠BAF的度数,故可得出∠BAD的度数,再由直角三角形的性质即可得出结论;
(2)由(1)知,∠BCE=30°,故可得出BC=2BE,再由三角形的面积公式即可得出结论.
【解答】解:(1 )∵AD,CE是高线,
)∵AD,CE是高线,
∴∠BEC=∠ADB=∠ADC=90°.
∴∠DAF=90°﹣∠AFD=90°﹣80°=10°.
∵AF平分∠BAC,
∴∠BAF= ∠BAC=
∠BAC= ×80°=40°.
×80°=40°.
∴∠BAD=∠BAF﹣∠DAF=40°﹣10°=30°.
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BCE=∠BAD=30°.

(2)在Rt△BCE中,
∵∠BCE=30°,
∴BC=2BE=2×5=10.
∴S△ABC= BC•AD=
BC•AD= ×10×6=30.
×10×6=30.
【点评】本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(﹣1,a),B(3,a),且最低点的纵坐标为﹣4.
(1)求抛物线的表达式及a的值;
(2)设抛物线顶点C关于y轴的对称点为点D,点P是抛物线对称轴上一动点,记抛物线在点A,B之间的部分为图象G(包含A,B两点),如果直线DP与图象G恰好有两个公共点,结合函数图象,求点P纵坐标t的取值范围.
(3)抛物线上有一个动点Q,当点Q在该抛物线上滑动到什么位置时,满足S△QAB=12,并求出此时Q点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
对于二次函数y=2(x﹣1)2﹣3的图象性质,下列说法不正确的是( )
A.开口向上 B.对称轴为直线x=1
C.顶点坐标为(1,﹣3) D.最小值为3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知一次函数y=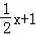
 的图象与x轴交于A点,与y轴交于B点:抛物线y=
的图象与x轴交于A点,与y轴交于B点:抛物线y=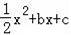
 的图象余一次函数y=
的图象余一次函数y=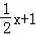
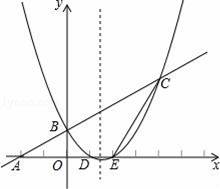
 的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
的图象交于B、C两点,与x轴交于D、E两点,且点D的坐标为(1,0).
(1)求点B的坐标;
(2)求该抛物线的解析式;
(3)求四边形BDEC的面积S;
(4)在x轴上是否存在点P,使得以点P、B、C为顶点的三角形是直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com