
分析 设第一批衬衫每件进价为x元,则第二批每件进价为(x-10)元.根据第二批该款式的衬衫,进货量是第一次的一半,列出方程即可解决问题.
解答 解:设第一批衬衫每件进价为x元,则第二批每件进价为(x-10)元.
由题意:$\frac{4500}{x}$×$\frac{1}{2}$=$\frac{2100}{x-10}$,
解得:x=150,
经检验x=150是原方程的解,且符合题意,
$\frac{4500}{150}$=30件,$\frac{2100}{150-10}$=15件,
答:两次分别购进这种衬衫30件和15件.
点评 本题考查分式方程的应用,解题的关键是学会设未知数、找等量关系、列出方程解决问题,注意分式方程必须检验,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
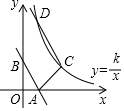 如图,已知直线l:y=-2x+2与x轴、y轴交于A、B两点,平移直线l交y=$\frac{k}{x}$于C、D两点,且CD=2AB,若AC=5,求D点坐标及k的值.
如图,已知直线l:y=-2x+2与x轴、y轴交于A、B两点,平移直线l交y=$\frac{k}{x}$于C、D两点,且CD=2AB,若AC=5,求D点坐标及k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
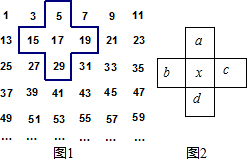 如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com