图（A）、图（B）、图（C）是三张形状、大小
完全相同的方格纸，方格纸中的每个小正方形的边长均为1．请在图（A）、图（B）、图（C）中，分别画出符合要求的图形，所画图形各顶点必须与方格纸中的小正方形顶点重合．
具体要求如下：
（1）画一个底边长为4，面积为8的等腰三角形；
（2）画一个面积为10的等腰直角三角形；
（3）画一个一边长为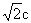
，面积为6的等腰三角形．
阅读快车系列答案科目：初中数学 来源： 题型：
教师节到了，为了表示对老师的敬意，小明做了两幅大小不同的正方形壁画送给老师，其中
一幅面积为800cm2，另一幅面积为450cm2，他想如果再用金彩带把两幅壁画的边镶上会更漂亮，他现在有1.2m长的金彩带，请你帮忙算一算，他的金彩带够用吗? 如果不够用，还需买多长的金彩带? （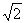
≈1.414，结果保留整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
能够成为直角三角形三条边长的三个正整数，我们称之为勾股数，观察下列表格所给的三个数a，b，c，a＜b＜c．
（1）试找出它们的共同点，并证明你的结论；
（2）写出当a＝17时，b，c的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，E、F是平行四边形对角线AC上的两点，并且AE＝CF．求证：四边形BFDE是平行四边形．判定平行四边形的方法很多，在具体应用时，到底
用哪种方法更好呢？
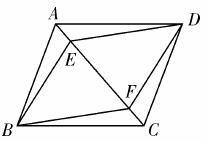
小明、小华、小
颖三位同学对此题进行探讨，给出了各自不同的证明如下：
小明的证明方法：
∵ 四边形ABCD是平行四边形，
∴ AD∥BC，AD＝BC．
∴ ∠DAE＝∠BCF．
又 AE＝CF，
∴ △AED≌△CFB．
∴ DE＝BF，∠AED＝∠CFB．
∴ ∠DEF＝∠BFE．
∴ 
ED∥BF．
∴ 四边形BEDF是平行四边形．
小华的证明方法：
∵ 四边形ABCD是平行四边形，
∴ AD∥BC，AD＝BC．
∴ ∠DAE＝∠BCF．
又 AE＝CF，
∴ △AED≌△CFB．
∴ DE＝BF．
同理可证△ABE≌△CDF．
∴ BE＝DF．
∴ 四边形BEDF是平行四边形．
小颖的证明方法：
如图，连接BD交AC于点O．
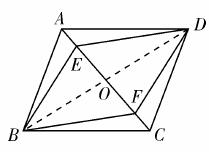
∵ 四边形ABCD是平行四边形，
∴ AO＝OC，BO＝OD．
又 AE＝CF，
∴ OE＝OF．
由BO＝OD，OE＝OF知四边形BEDF是平行四边形．
就这三名同学的证明方法，你认为哪一种方法最为简捷？从中你得到什么启示？
查看答案和解析>>
科目：初中数学 来源： 题型：
某活动小组为使全小组成员的成绩都要达到优秀，打算实施“以优帮差”计划，为此统计了上次测试各成员的成绩（单位：分）：90，95，87，92，63，54，82
，76，55，100，45，80．计算这组数据的极差，这个极差说明了什么问题？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
