
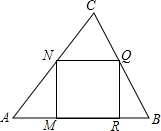
 如图,已知正方形MNQR内接于锐角△ABC中,设△ABC的面积为S,正方形MNQR的面积为S1,求证:S1≤$\frac{1}{2}$S.
如图,已知正方形MNQR内接于锐角△ABC中,设△ABC的面积为S,正方形MNQR的面积为S1,求证:S1≤$\frac{1}{2}$S. 分析 由NQ∥AB知△NCQ∽△ABC,设△ABC的底边AB=a,底边上的高为h,正方形的边长为m,利用相似三角形的对应高的比等于相似比,表示出出正方形的边长,根据不等式的性质得出结论.
解答 解:设△ABC的底边AB=a,底边上的高为h,正方形的边长为m,
∴S=$\frac{1}{2}$ah,
∵NQ∥AB ,
,
∴△NCQ∽△ABC,
∴$\frac{m}{a}=\frac{h-m}{h}$,
∴m=$\frac{ah}{a+h}$,
∴S1=($\frac{ah}{a+h}$)2,
根据不等式的性质知:a+h≥2$\sqrt{ah}$,
∴S1=($\frac{ah}{a+h}$)2≤($\frac{ah}{2\sqrt{ah}}$)2=$\frac{1}{4}ah$=$\frac{1}{2}$S,
即S1≤$\frac{1}{2}$S.
点评 本题考查了相似三角形的判定与性质的综合运用,利用不等式的性质得到a+h≤2$\sqrt{ah}$,是解决问题的关键所在.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
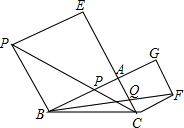 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
| n | 7 | 8 | 9 | 10 |
| m | 2 | 1 | 2 | 2 |
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m | k | k-1 | k | k |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m2+m2=m4 | B. | (m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$ | C. | (3mn2)2=6m2n4 | D. | 2m2n÷$\frac{m}{n}$=2mn2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为$\frac{3}{4}$.
如图,有四张不透明的卡片除正面的函数关系式不同外,其余相同,将它们背面朝上洗匀后,从中抽取一张卡片,则抽到函数图象不经过第四象限的卡片的概率为$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com