

分析 图,作DM⊥AC于M,DH⊥BC于H,DN⊥EB于N,连接DF.首先证明△DFB≌△DFC,推出CF=BF,推出△EFC的周长=EF+CF+EC=(EF+FB)+EC=EB′+EC=CB′,由此即可解决问题.
解答 解:如图,作DM⊥AC于M,DH⊥BC于H,DN⊥EB于N,连接DF.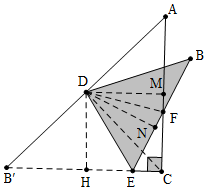
∵CA=CB,∠ACB=90°,AD=B′D,
∴CD=DB′=AD=DB,∠DCB=∠DCA=45°,∠B′=∠B=∠DCA=45°.
∴DH=DM=DN,
∴∠DFM=∠DFN,
∵∠BFM=∠EFC,
∴∠DFB=∠DFC,
在△DFB和△DFC中,
$\left\{\begin{array}{l}{∠B=∠DCF}\\{∠DFB=∠DFC}\\{DF=DF}\end{array}\right.$,
∴△DFB≌△DFC,
∴CF=BF,
∵△EFC的周长=EF+CF+EC=(EF+FB)+EC=EB′+EC=CB′,
∵AB′=$\sqrt{10}$,
∴CB′=AB′•cos45°=$\sqrt{10}$×$\frac{\sqrt{2}}{2}$=$\sqrt{5}$,
故答案为$\sqrt{5}$.
点评 本题考查翻折变换、等腰直角三角形的性质、全等三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
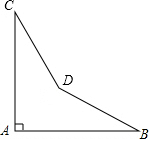 某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
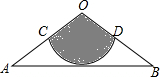 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为20$\sqrt{2}$cm.
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为20$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com