
分析 根据根的判别式的意义得到△=4(k+2)2-4(2k2+7)=0,解得k1=1,k2=3,当k=1时,方程为x2-6x+9=0,利用根与系数得到两腰之和为6,不符合三角形三边的关系,舍去;所以k=3.
解答 解:∵方程x2-2(k+2)x+2k2+7=0有两个相等的两根,
∴△=4(k+2)2-4(2k2+7)=0,
整理得k2-4k+3=0,解得k1=1,k2=3,
当k=1时,方程为x2-6x+9=0,两根之和为6,而6<7,舍去;
当k=3时,方程为x2-10x+25=0,两根之和为10,而10>7,
∴k的值为3.
故答案为3.
点评 本题考查了根与系数的关系:若二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
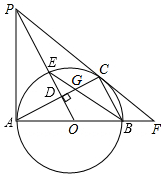 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P.连接BE交AC于G,连接PC并延长AB的延长线交于点F,BF=3,CF=4.
如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P.连接BE交AC于G,连接PC并延长AB的延长线交于点F,BF=3,CF=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
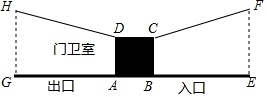 如图,这是一传媒公司寓意为“大鹏展翅”的大门建筑截面图,它是两条关于顶点成中心对称的抛物线,开口朝向左右,顶点为边长为4米的正方形中心,且分别过正方形的两个顶点.若入口水平宽BE为10.5米,则最高点F到地面的高度FE为7米.
如图,这是一传媒公司寓意为“大鹏展翅”的大门建筑截面图,它是两条关于顶点成中心对称的抛物线,开口朝向左右,顶点为边长为4米的正方形中心,且分别过正方形的两个顶点.若入口水平宽BE为10.5米,则最高点F到地面的高度FE为7米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com