
����Ŀ��Ϊ�˸��õı�������ͼ��������ʪ�أ���������ˮ�����������ȹ���A��B������ˮ�����豸��20̨��������ʪ���ܱ���ˮ���д�����ÿ̨A����ˮ�����豸12��Ԫ��ÿ̨B����ˮ�����豸10��Ԫ����֪1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬����ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
���𰸡���1��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200������2���������ַ������������������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��
����������1����A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣���![]() �������
�������![]() ��
��
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���蹺��A����ˮ�����豸x̨������B����ˮ�����豸��20��x��̨������![]() �������12.5��x��15���������ַ�����
�������12.5��x��15���������ַ�����
��һ�ַ�������x=13ʱ��20��x=7�����ѵķ���Ϊ��13��12+7��10=226��Ԫ��
�ڶ��ַ�������x=14ʱ��20��x=6�����ѵķ���Ϊ��14��12+6��10=228��Ԫ��
�����ַ�������x=15ʱ��20��x=5�����ѵķ���Ϊ��15��12+5��10=230��Ԫ��
������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=x��1��ͼ��ƽ�ƺ��㣨��4��2������ʱ����ͼ������������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ���Ķ����������ģ��ö��飬�����飬�����������森Ϊ����ͬѧ�ǵĶ�������ѧУͼ��������»����ɹ���ѧ�����Ͷ���������ͼ�飮���˽⣬20����ѧ������40�������鹲��1520Ԫ��20����ѧ������20���������440Ԫ��ע�����ɹ�����ѧ�����۸�һ�������ɹ��Ķ�����۸�һ������
��1����ÿ����ѧ�����Ͷ����������Ԫ��
��2����ѧУҪ�����������ѧ������20�������������ѧ��������������72�����ܷ��ò�����2000Ԫ����������з��������Ĺ��鷽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⡿
����֪��1+2+3+��+n= ![]() ����ô12+22+32+��+n2������ڶ����أ�
����ô12+22+32+��+n2������ڶ����أ�
��ͼ1��ʾ�����������У���1��ԲȦ�е���Ϊ1����12 �� ��2������ԲȦ�����ĺ�Ϊ2+2����22 �� ������ n�� n��ԲȦ�����ĺ�Ϊ ![]() ����n2 ���������������������й���
����n2 ���������������������й��� ![]() ��ԲȦ������ԲȦ�����ĺ�Ϊ1+2+3+��+n2.
��ԲȦ������ԲȦ�����ĺ�Ϊ1+2+3+��+n2.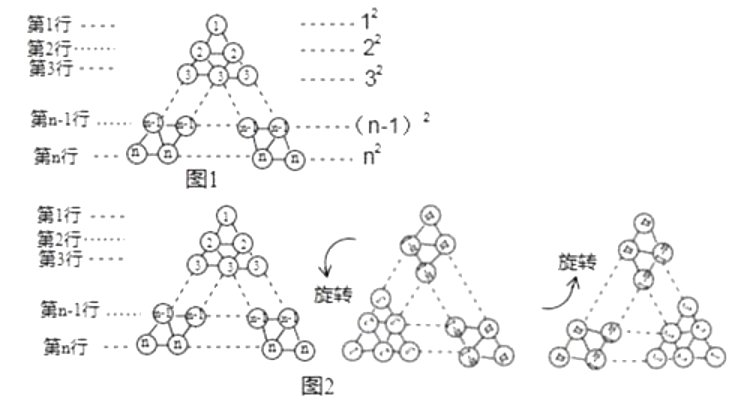
��1��������̽����
������������������ת�ɵ���ͼ 2 ��ʾ�����������۲��������������������ͬһλ��ԲȦ�е�������� n��1�еĵ�һ��ԲȦ�е����ֱ�Ϊ n��1��2��n��������ÿ��λ��������ԲȦ�����ĺ;�Ϊ �� �ɴ˿ɵã���������������������ԲȦ�������ܺ�Ϊ3��12+22+32+��+n2��= �� ���12+22+32+��+n2=��
��2����������⡿
�������Ϸ��֣����㣺 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
����1����һԪ���η���ax2+bx+c=0��a��0��������Ϊx1 �� x2 �� ��x1+x2=![]() �� x1x2=
�� x1x2=![]() ��
��
����2����֪ʵ��m��n����m2��m��1=0��n2��n��1=0����m��n����![]() ��ֵ��
��ֵ��
�⣺����֪m��n�Ƿ���x2��x��1=0����������ȵ�ʵ���������ݲ���1��
m+n=1��mn=��1
��![]() =
=![]()
�����������Ͻ���������⣺
��1��һԪ���η���2x2+3x��1=0������Ϊx1��x2 �� ��x1+x2= �� x1x2= ��
��2����֪ʵ��m��n����2m2��2m��1=0��2n2��2n��1=0����m��n����m2n+mn2��ֵ��
��3����֪ʵ��p��q����p2=3p+2��2q2=3q+1����p��2q����p2+4q2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬С�Ź���100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���

��1��С����ν�����ʹ������ǡ��Ϊ1300Ԫ��
��2��Ҫʹ�����ľ�����������������������������۸��40%�������С�����һ�������������������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����������ڲ����߶��ǣ� ��
A.�����εĽ�ƽ���ߣ�
B.�����ε����ߣ�
C.�����εĸߣ�
D.�����ε���λ�ߡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������⡣
��1����֪��x��1����ƽ�����ǡ�3����x��2y+1������������3����x2��y2��ƽ������
��2����֪y= ![]() +
+ ![]() ��8����
��8���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com