
【题目】阅读材料:
材料1、若一元二次方程ax2+bx+c=0(a≠0)的两根为x1 , x2 , 则x1+x2=![]() , x1x2=
, x1x2=![]() .
.
材料2、已知实数m、n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m、n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得
m+n=1,mn=﹣1
∴![]() =
=![]()
根据上述材料解决下面问题:
(1)一元二次方程2x2+3x﹣1=0的两根为x1、x2 , 则x1+x2= , x1x2= .
(2)已知实数m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p、q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.
【答案】解:(1)x1+x2=﹣![]() , x1x2=﹣
, x1x2=﹣![]() ;
;
故答案为﹣![]() , ﹣
, ﹣![]() ;
;
(2)∵m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,
∴m、n可看作方程2x2﹣2x﹣1=0的两实数解,
∴m+n=1,mn=﹣![]() ,
,
∴m2n+mn2=mn(m+n)=﹣![]() ×1=﹣
×1=﹣![]() ;
;
(3)设t=2q,代入2q2=3q+1化简为t2=3t+2,
则p与t(即2q)为方程x2﹣3x﹣2=0的两实数解,
∴p+2q=3,p2q=﹣2,
∴p2+4q2=(p+2q)2﹣2p2q=32﹣2×(﹣2)=13.
【解析】(1)直接根据根与系数的关系求解;
(2)利用m、n满足的等式,可把m、n可看作方程2x2﹣2x﹣1=0的两实数解,则根据根与系数的关系得到m+n=1,mn=﹣![]() , 接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
, 接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
(3)先设t=2q,代入2q2=3q+1化简得到t2=3t+2,根据p与t满足的等式可把p与t(即2q)为方程x2﹣3x﹣2=0的两实数解,则根据根与系数的关系得到p+2q=3,p2q=﹣2,接着利用完全平方公式变形得到p2+4q2=(p+2q)2﹣2p2q,然后利用整体代入的方法计算.
【考点精析】掌握根与系数的关系是解答本题的根本,需要知道一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


科目:初中数学 来源: 题型:
【题目】(列方程(组)及不等式解应用题)
春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的表示集合的大括号内:
-3,- ![]() ,0.31,-(-2),
,0.31,-(-2), ![]() ,-1.4,1.732,
,-1.4,1.732, ![]() ,0,1.1010010001……(每两个1之间依次多一个 0)
,0,1.1010010001……(每两个1之间依次多一个 0)
正有理数{…};
整数{…};
负分数{…} ;
无理数{…};
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,纸上有五个边长为 1 的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.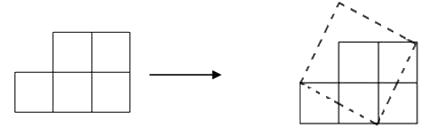
(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1 点为圆心, 直角三角形的最大边为半径画弧,交数轴正半轴于点 A,那么点 A 表示的数是多少? 点 A 表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑摩托车从 ![]() 地去
地去 ![]() 地,乙开汽车从
地,乙开汽车从 ![]() 地去
地去 ![]() 地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为
地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为 ![]() (单位:千米),甲行驶的时间为
(单位:千米),甲行驶的时间为 ![]() (单位:小时),
(单位:小时), ![]() 与
与 ![]() 之间的函数关系如图所示,有下列结论:
之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )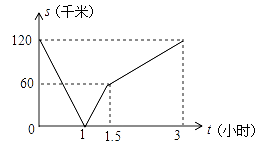
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com