
【题目】如图,在边长为8的等边△BCD中,DF⊥BC于点F,点A为射线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,求证:DA=CE;
(2)当∠DEC=45°时,连接AC,求四边形ABDC的面积;
(3)连接EF,当EF取得最小值时,线段AB的长是多少?(只写答案,不要过程)

【答案】(1)证明见解析;(2)32;(3)![]() .
.
【解析】
(1)根据旋转的性质、等边三角形的性质由SAS证明△BAD≌△BEC即可得出结论;
(2)先证明∠DCE=∠BCE+∠BCD=90°,由∠DEC=45°,证得△DCE是等腰直角三角形,从而可得CE的长,即为DA的长,进一步即可得出结果;
(3)由前面的结论知:在点A运动的过程中,始终保持∠BCE=30°不变,即点E在射线CE上运动,于是当EF⊥CE时,EF取得最小值,过点E作EG⊥BC于点G,如图2所示,利用30°的直角三角形的性质和勾股定理可求出BE的长,即为AB的长,问题即得解决.
(1)证明:∵把BA顺时针方向旋转60°至BE,
∴BA=BE,∠ABE=60°,
在等边△BCD中,DB=BC,∠DBC=60°,
∴∠DBA=∠DBC+∠FBA=60°+∠FBA,
∵∠CBE=60°+∠FBA,
∴∠DBA=∠CBE,
在△BAD和△BEC中,∵BA=BE,∠DBA=∠CBE,DB=BC ,
∴△BAD≌△BEC(SAS),
∴DA=CE;
(2)解:如图1所示:∵DB=DC,DA⊥BC,
∴∠BDA=![]() ∠BDC=30°,
∠BDC=30°,
∵△BAD≌△BEC,∴∠BCE=∠BDA=30°,
在等边△BCD中,∵∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=30°+60°=90°,
∵∠DEC=45°,
∴△DCE是等腰直角三角形,
∴CE=CD=8,
由(1)得:DA=CE,
∴DA=CE=8,
∵DF⊥BC,
∴四边形ABDC的面积=![]() BC×AD=
BC×AD=![]() ×8×8=32;
×8×8=32;
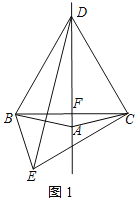
(3)由(2)知∠BCE=∠BDA=30°,
∴在点A运动的过程中,始终保持∠BCE=30°不变,即点E在射线CE上运动,
∴当EF⊥CE时,EF取得最小值,过点E作EG⊥BC于点G,如图2所示:
∵△BCD是等边三角形,DF⊥BC,
∴BF=CF=![]() BC=4,
BC=4,
∵∠BCE=∠FEG=30°,
∴EF=![]() CF=2,
CF=2,
∴FG=![]() EF=1,EG=
EF=1,EG=![]() EF=
EF=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
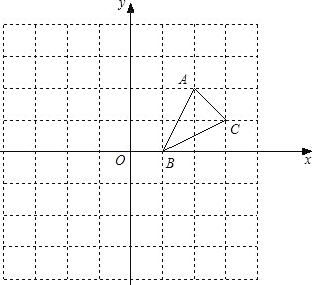
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察发现;如图1,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() .填空:
.填空:
①![]() 与
与![]() 是否相似? (直接回答)______;
是否相似? (直接回答)______;
②![]() _______;
_______; ![]() .
.
(2)拓展探究:将![]() 绕顶点
绕顶点![]() 旋转到图2所示的位置,猜想
旋转到图2所示的位置,猜想![]() 与
与![]() 是否相似?若不相似,说明理由;若相似,请证明.
是否相似?若不相似,说明理由;若相似,请证明.
(3)迁移应用:将![]() 绕顶点
绕顶点![]() 旋转到点
旋转到点![]() 在同一条直线上时,直接写出线段
在同一条直线上时,直接写出线段![]() 的长是 .
的长是 .
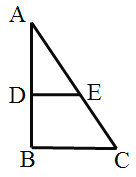
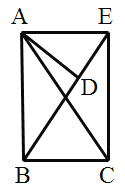
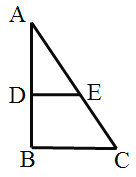
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创客联盟的队员想用3D的打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
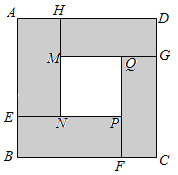
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1700元购买材料一定够用吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.
(1)分别求出y1、y2与x的函数关系式,并确定x的取值范范围;
(2)分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)
(3)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点c直线y=﹣x+4经过点B、C.
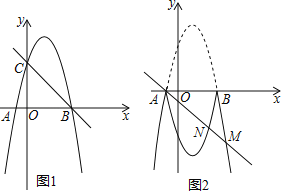
(1)求抛物线的表达式;
(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC的面积,求点M的坐标;
(3)如图2,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com