
(本小题满分8分)
已知抛物线y=ax2+bx+6与x轴交于A、B两点(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OB= OC,tan∠ACO=
OC,tan∠ACO=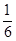 ,顶点为D.
,顶点为D.
1.(1)求点A的坐标.
2.(2)求直线CD与x轴的交点E的坐标.
3.(3)在此抛物线上是否存在一点F,使得以点A、C、E、F为顶点的四边形是平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
4.(4)若点M(2,y)是此抛物线上一点,点N是直线AM上方的抛物线上一动点,当点N运动到什么位置时,四边形ABMN的面积S最大? 请求出此时S的最大值和点N的坐标.
5.(5)点P为此抛物线对称轴上一动点,若以点P为圆心的圆与(4)中的直线AM及x轴同时相切,则此时点P的坐标为 .
1.解:(1)根据题意,得C(0,6).
在Rt△AOC中,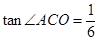 ,OC=6,
,OC=6,
∴OA=1. ∴A(-1,0)
2.(2)∵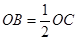 ,∴OB=3. ∴B(3,0).
,∴OB=3. ∴B(3,0).
由题意,得  解得
解得 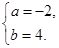
∴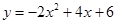 .
.
∴D(1,8). ……………………………………………………………………2分
可求得直线CD的解析式为 .
.
∴E(-3,0).
3.(3)假设存在以点A、C、F、E为顶点的平行四边形,
则F1(2,6),F2(-2,6),F3(-4,-6).
经验证,只有点(2,6)在抛物线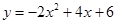 上,
上,
∴F(2,6)
4.(4)如图,作NQ∥y轴交AM于点Q,设N(m, 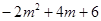 ).
).
当x=2时,y=6,∴M(2,6).
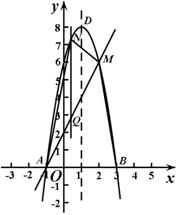 可求得直线AM的解析式为
可求得直线AM的解析式为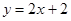 .
.
∴Q(m,2m+2).
∴NQ=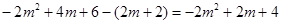 .
.
∵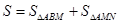 ,其中
,其中 ,
,
∴当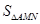 最大时,
最大时, 值最大.
值最大.
∵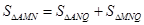
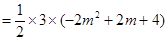 ,
,
 ,
,
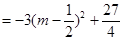 .
.
∴当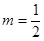 时,
时,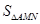 的最大值为
的最大值为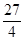 .
.
∴ 的最大值为
的最大值为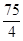 .……………………………………………………………………6分
.……………………………………………………………………6分
当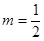 时,
时,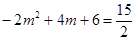 .
.
∴N(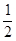 ,
,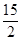 ).
).
5.(5)P1(1,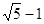 ),P2(1,
),P2(1,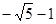 ). …………………………………………8分
). …………………………………………8分
说明:写成P1(1,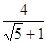 ),P2(1,
),P2(1,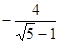 )不扣分
)不扣分
【解析】略


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
 (本小题满分6分,请在下列两个小题中,任选其一完成即可)
(本小题满分6分,请在下列两个小题中,任选其一完成即可)查看答案和解析>>
科目:初中数学 来源: 题型:
| 13 |
| 13 |
| 13 |

查看答案和解析>>
科目:初中数学 来源:2011年湖北省荆州市芦陵中学中考模拟试题(二)数学卷 题型:解答题
(本小题满分8分)
据2010年5月8日《杭州日报》报道:今年“五一”黄金周期间,我市实现旅游收入再创历史新高,旅游消费呈现多样化,各项消费所占的比例如图秘所示,其中住宿消费为3438.24万元.
(1)求我市今年“五一”黄金周期间旅游消费共多少亿元?旅游消费中各项消费的中位数是多少万元?
(2)对于“五一”黄金周期间的旅游消费,如果我市2012年要达到3.42亿元的目标,那么,2010年到2012年的平均增长率是多少?
2010年杭州市“五一”黄金周旅游各项消费分布统计图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com