
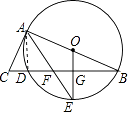
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线. 
(1)求证:∠ACB=2∠EAB;
(2)若cos∠ACB= ![]() ,AC=10,求BF的长.
,AC=10,求BF的长.
【答案】
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AC是⊙O的切线,
∴∠CAB=90°,
∴∠C+∠CAD=∠CAD+∠DAB=90°,
∴∠C=∠DAB,
∵OE⊥BD,
∴2 ![]() =
= ![]() ,
,
∴∠BAE= ![]() BDA,
BDA,
∴∠ACB=2∠EAB
(2)解:∵cos∠ACB= ![]() ,AC=10,
,AC=10,
∴BC=25,
∴AB= ![]() =5
=5 ![]() ,
,
∵∠C=∠BAD,∠B=∠B,
∴△ABC∽△DBA,
∴ ![]() ,
,
∴BD= ![]() =21,
=21,
∵OE⊥BD,
∴BG=DG= ![]() ,
,
∵AD= ![]() =2
=2 ![]() ,
,
∵AO=BO,BG=DG,
∴OG= ![]() AD=
AD= ![]() ,
,
∴GE= ![]() ,
,
∵AD∥GE,
∴ ![]() =
= ![]() ,
,
∴FG= ![]() DG=
DG= ![]() ,
,
∴BF=BG+FG= ![]() +
+ ![]() =15.
=15.
【解析】(1)连接AD,由AB是⊙O的直径,得到∠ADB=90°,由AC是⊙O的切线,得到∠CAB=90°,根据余角的性质得到∠C=∠DAB,根据圆周角定理即可得到结论;(2)根据三角函数的定义得到BC=25,根据勾股定理得到AB= ![]() =5
=5 ![]() ,根据相似三角形的性质得到BD=
,根据相似三角形的性质得到BD= ![]() =21,根据垂径定理得到BG=DG=
=21,根据垂径定理得到BG=DG= ![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到 ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】本题主要考查了垂径定理和切线的性质定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,要是四边形ABCD成为平行四边形,则应增加的条件是( ) 
A.AB=CD
B.∠BAD=∠DCB
C.AC=BD
D.∠ABC+∠BAD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)若该抛物线经过原点O,且a=﹣ ![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在(1)的条件下,点P(m,n)在抛物线上,且∠POB锐角,满足∠POB+∠BCD<90°,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)
(1)当点P的坐标为(﹣1,0)时,求点D的坐标;
(2)点P在移动的过程中,点D是否在直线y=x﹣2上?请说明理由;
(3)连接OB交AD于点G,求证:AG=DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点. 
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 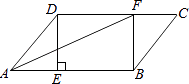
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com