
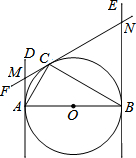
 如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )
如图.已知AB为⊙O的直径,AB=2,AD和BE是⊙O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,则AM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{3}$ |
分析 连接OM,OC,由OB=OC,且∠ABC的度数求出∠BCO的度数,利用外角性质求出∠AOC度数,利用切线长定理得到MA=MC,利用HL得到三角形AOM与三角形COM全等,利用全等三角形对应角相等得到OM为角平分线,求出∠AOM为30°,在直角三角形AOM中,利用锐角三角函数定义即可求出AM的长.
解答 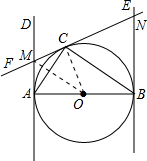 解:连接OM,OC,
解:连接OM,OC,
∵OB=OC,且∠ABC=30°,
∴∠BCO=∠ABC=30°,
∵∠AOC为△BOC的外角,
∴∠AOC=2∠ABC=60°,
∵MA,MC分别为圆O的切线,
∴MA=MC,且∠MAO=∠MCO=90°,
在Rt△AOM和Rt△COM中,
$\left\{\begin{array}{l}MA=MC\\ OM=OM\end{array}\right.$,
∴Rt△AOM≌Rt△COM(HL),
∴∠AOM=∠COM=$\frac{1}{2}$∠AOC=30°,
在Rt△AOM中,OA=$\frac{1}{2}$AB=1,∠AOM=30°,
∴tan30°=$\frac{AM}{OA}$,即$\frac{\sqrt{3}}{3}$=$\frac{AM}{1}$,
解得:AM=$\frac{\sqrt{3}}{3}$.
故选A.
点评 此题考查了切线的性质,锐角三角函数定义,外角性质,以及等腰三角形的性质,熟练掌握切线的性质是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中非峰会,中国政府承诺向非洲提供总额600亿美元的资金支持其发展,将600亿用科学记数法表示为6×1011 | |
| B. | 在一个只装有白球和红球的袋中摸球,摸出红球是必然事件 | |
| C. | 在比例尺为1:100000的地图上,量得甲、乙两地的距离是15cm,则两地的实际距离是15km | |
| D. | 任意三角形都有外接圆和内切圆,它们是同心圆 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
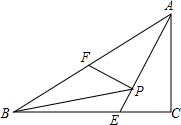 如图,在△ABC中,∠ACB=90°,AC=4,∠B=30°,F为AB的中点,AE平分∠BAC,点P为线段AE上一动点,当△BFP周长最小为4+4$\sqrt{3}$时,S△ABC=8$\sqrt{3}$.
如图,在△ABC中,∠ACB=90°,AC=4,∠B=30°,F为AB的中点,AE平分∠BAC,点P为线段AE上一动点,当△BFP周长最小为4+4$\sqrt{3}$时,S△ABC=8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com