
【题目】如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求∠ADB的大小;
(2)求B、D之间的距离;
(3)求C、D之间的距离.
【答案】解:(1)∵∠EAB=∠EAD+∠DAC=45°+15°=60°,
又∵AE∥BF,
∴∠ABF=180°-∠EAB=120°,
∴∠ABD=∠ABF+∠FBD=120°+30°=150°,
∴∠ADB=180°-∠DAC-∠ABD=180°-15°-150°=15°;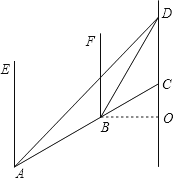
(2)由(1)可知∠ADB=15°,
∵∠DAC=15°,
∴∠DAC=∠ADB=15°,
∴BD=AB=2km.
即B,D之间的距离是2km;
(3)过B作BO⊥DC,交DC的延长线于点O,
在Rt△DBO中,BD=2km,
∵∠FBD=30°,
∴∠DBO=60°,
∴DO=2×sin60°=![]() (km),BO=2×cos60°=1,
(km),BO=2×cos60°=1,
在Rt△CBO中,
∵∠BCO=∠EAC=60°,
∴∠CBO=30°,CO=BO×tan30°=![]() ,
,
∴CD=DO-CO=![]() -
-![]() =
=![]() (km).
(km).
即C,D之间的距离![]() km.
km.
【解析】(1)根据平行线的性质,以及方向角的定义即可求解;
(2)根据等角对等边,即可证得BD=AB即可求解;
(3)根据等角对等边即可证得BC=CD,然后根据三角函数即可求得CD的长.
【考点精析】利用关于方向角问题对题目进行判断即可得到答案,需要熟知指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.


科目:初中数学 来源: 题型:
【题目】某“爱心义卖”活动中,购进甲、乙两种文具,甲每个进货价高于乙进货价10元,90元买乙的数量与150元买甲的数量相同.
(1)求甲、乙进货价;
(2)甲、乙共100件,将进价提高20%进行销售,进货价少于2080元,销售额要大于2460元,求有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
A.1.2米
B.1.5米
C.1.9米
D.2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30° . 已知楼房高AB约是45m , 根据以上观测数据可求观光塔的高CD是m . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
(1)图中有哪几对位似三角形,选其中一对加以证明;
(2)若AB=2,CD=3,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com