
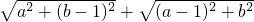 的最小值为________.
的最小值为________.
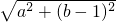 ,A和C之间的距离是AC=
,A和C之间的距离是AC=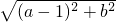 ,求出AB+AC=
,求出AB+AC=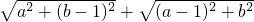 ,即求出AB+AC的最小值,根据两点之间线段最短得出AC+AB的最小值是AB+AC=BC,即最小值是BC的长,求出BC即可.
,即求出AB+AC的最小值,根据两点之间线段最短得出AC+AB的最小值是AB+AC=BC,即最小值是BC的长,求出BC即可.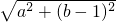 ,
,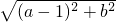 ,
,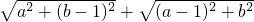 ,
,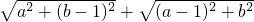 的最小值可以看作求出AB+AC的最小值,即点A(a,b)到B(0,1)和C(1,0)的距离和最短的地方,根据两点之间线段最短,
的最小值可以看作求出AB+AC的最小值,即点A(a,b)到B(0,1)和C(1,0)的距离和最短的地方,根据两点之间线段最短,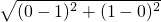 =
= ,
,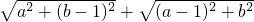 的最小值是
的最小值是 ,
, .
.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源:2010年江苏省苏州市昆山市九年级(下)数学调研测试卷(解析版) 题型:填空题
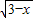 +
+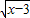 ,则|x-y|的值是 .
,则|x-y|的值是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com