
【题目】在平面直角坐标系中,点![]() 为坐标原点,已知点
为坐标原点,已知点![]() ,将
,将![]() 绕坐标原点
绕坐标原点![]() 旋转90°到
旋转90°到![]() ,则点
,则点![]() 的坐标是__________.
的坐标是__________.
【答案】![]() 或
或![]()
【解析】
根据题意作图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标,同理求出逆时针旋转90![]() 时A′的坐标,故可求解.
时A′的坐标,故可求解.
如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,

∵OA绕坐标原点O顺时针旋转90![]() 至OA′,
至OA′,
∴OA=OA′,∠AOA′=90![]() ,
,
∵∠A′OB′+∠AOB=90![]() ,∠AOB+∠OAB=90
,∠AOB+∠OAB=90![]() ,
,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
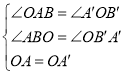 ,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(4,3).
同理OA绕坐标原点O逆时针旋转90![]() 至OA′
至OA′
OB’=AB=4,A’B’=OB=3
∴点A′的坐标为(-4,3).
综上,点A′的坐标为(4,3)或(-4,3).
故答案为:![]() 或
或![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,
中, ![]() ,AB=BC,A,B的坐标分别为
,AB=BC,A,B的坐标分别为 ![]() ,将
,将 ![]() 绕点P旋转
绕点P旋转 ![]() 后得到
后得到 ![]() ,其中点B的对应点
,其中点B的对应点 ![]() 的坐标为
的坐标为 ![]() .
.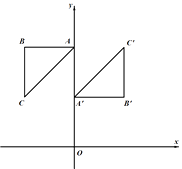
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数 ![]() (件)与价格
(件)与价格 ![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.
(1)购买一支钢笔和一本笔记本各需多少钱?
(2)若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交
轴交 ![]() 、
、 ![]() 两点,直线
两点,直线 ![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.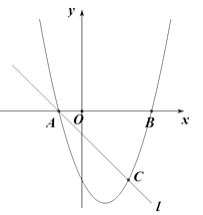
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 ![]() 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究: 如图,直线![]() 的表达式为
的表达式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的表达式;
的表达式;
(3)求![]() 的值;
的值;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出点
?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制如图所示的两幅不完整的统计图.

请结合图中所给出的信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图;
(3)若某商场天内有![]() 人次支付记录,估计选择微信支付的人数.
人次支付记录,估计选择微信支付的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com