

���� ��1����a=-1���������ߵĽ���ʽ��Ȼ����y=����ö�Ӧ��x��ֵ���Ӷ��ɵõ�p1�����꣬Ȼ������ƽ�Ƶķ���;���ɵõ���P2�����꣬�������������䷽������������ߵĶ���F1������ڸ��ݸá����������ߡ���������������ֱ�Ϊ1��-1���ɵó����ۣ�
��2����OQ�е�ΪO�䣬���߶�TnTn+1����O�䣬�ٸ���ͼ��ƽ�Ƶ����ʼ��ɵó����ۣ�
��� �⣺��1���ٵ�a=-1ʱ��y=ax2+2ax=-x2-2x��
��-x2-2x=0����ã�x=0��x=-2��
���P1��������-2��0����
��ƽ�Ƶ����ʿ�֪P2������Ϊ��2��0����
��y=-x2-2x=��x+1��2+1��
��ͼ��F1�Ķ�������Ϊ����-1��1����
�ڡ߸á����������ߡ���������������ֱ�Ϊ1��-1��
���H��2015��-2�������ڸá����������ߡ��ϣ�
��ͼ��Fn�Ķ���Tn�ĺ�����Ϊ201��
201��4=50��1������ͼ����F2��F4����״��ͬ��
��ͼ��Fn��Ӧ�Ľ���ʽΪ��y=��x-201��2-1��
���Ա���x��ȡֵ��ΧΪ��200��x��202��
��2����OQ�е�ΪO�䣬���߶�TnTn+1����O�䣬
�������֪OO��=O��Q��O��Tn=O��Tn+1��
�൱TnTn+1=OQ=12ʱ���ı���OTnTn+1QΪ���Σ�
��O��Tn+1=6��
��F1��Ӧ�Ľ���ʽΪy=a��x+1��2-a��
��F1�Ķ�������Ϊ��-1��-a����
����ƽ�Ƶ����ʿ�֪����Tn+1��������Ϊ-a��
���ɹ��ɶ����ã�-a��2+��-1��2=62��
��a=��$\sqrt{35}$��
��a��0��
��a=-$\sqrt{35}$���ʴ�ʱn��ֵΪ4��
���� ���⿼����Ƕ��κ����ۺ��⣬��֪���κ���ƽ�Ƶ����ʡ����κ�������ֵ�����ǽ�����Ĺؼ���


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
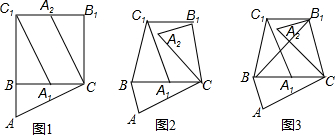
 ��ͼ����1=��2��BC=CE���벹��һ��������AC=DC��дһ�ּ��ɣ���ʹ�á�ABC�ա�DEC��
��ͼ����1=��2��BC=CE���벹��һ��������AC=DC��дһ�ּ��ɣ���ʹ�á�ABC�ա�DEC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36 | B�� | 37 | C�� | 38 | D�� | 40 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x$��\frac{1}{2}$ | B�� | x��-1 | C�� | -1��x��$\frac{1}{2}$ | D�� | x$��\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
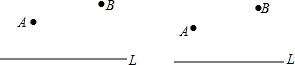
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������ | B�� | ������ | C�� | ������� | D�� | ˮ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com