
【题目】图①,图②都是4×6的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,且点A,B均在格点上.

(1)在图①中以AB为对角线画出一个矩形,使矩形的另外两个顶点也在格点上,且所画的矩形不是正方形;
(2)在图②中以AB为对角线画出一个菱形,使菱形的另外两个顶点也在格点上,且所画的菱形不是正方形;
(3)图①中所画的矩形的面积为 ;图②中所画的菱形的周长为 .
科目:初中数学 来源: 题型:
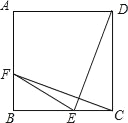
【题目】如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
(1)请画出旋转中心G (保留画图痕迹),并连接GF,GE;
(2)若正方形的边长为2a,当CE= 时,S△FGE=S△FBE;当CE= 时,S△FGE=3S△FBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
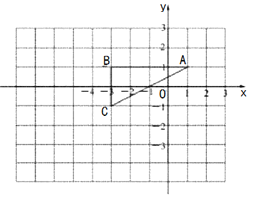
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1)、B(-3,1)、C(-3.-1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_________.
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为![]() 得到
得到![]() 在图中画出
在图中画出![]() 若将
若将![]() 沿
沿![]() 轴方向平移,需平移_______单位长度,能使得
轴方向平移,需平移_______单位长度,能使得![]() 所在的直线与⊙P相切.
所在的直线与⊙P相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
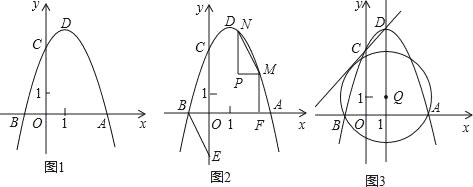
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
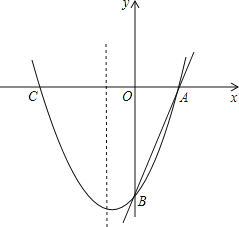
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:把一个自然数的个位数字截去,再用余下的数减去个位数的2倍,如果差是7的倍数,则原数能被7整除.如果差太大不易看出是否7的倍数,可重复上述「截尾、倍大、相减、验差」的过程,直到能清楚判断为止.例如,判断392是否7的倍数的过程如下:![]() ,
,![]() ,所以,392是7的倍数;又例如判断8638是否7的倍数的过程如下:
,所以,392是7的倍数;又例如判断8638是否7的倍数的过程如下:![]() ,
,![]() ,
,![]() ,所以,8638是7的倍数.
,所以,8638是7的倍数.
材料二:若一个四位自然数n满足千位与个位相同,百位与十位相同,我们称这个数为“对称数”.将“对称数”n的前两位与后两位交换位置得到一个新的“对称数”![]() ,记
,记![]() ,例如
,例如![]() .
.
(1)请用材料一的方法判断6909与367能不能被7整除;
(2)若m、p是“对称数”,其中![]() ,
,![]() (
(![]() ,
,![]() 且a,b,c均为整数),若m能被7整除,且
且a,b,c均为整数),若m能被7整除,且![]() ,求p.
,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
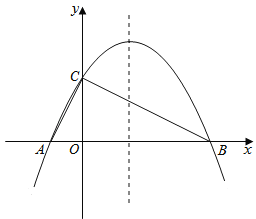
【题目】如图,已知抛物线y=﹣![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
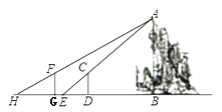
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com