
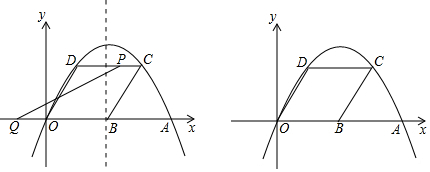
分析 (1)根据函数的解析式即可得到结论;
(2)①如图1,连接OC,OQ=t,DP=2t,根据已知条件得到四边形OBCD是平行四边形,推出四边形OBCD是菱形,根据菱形的想折叠的OC⊥BD,当E落在直线BD上时,PQ⊥BD,列方程即可得到结论;
②设DE交PQ于F,PQ交OD于G,当P在DC上时,DP<DC,DG<DO,则点E落在菱形OBCD内部,不可能落在x轴上,如图2,当P在BC上时,PC=2t-6,PB═12-2t,得到直线PQ的解析式为y=$\frac{\sqrt{3}(6-t)}{12}$x+$\frac{\sqrt{3}(6-t)}{12}$,若点E落在x轴上,设E(n,0),则点F是DE的中点,根据相似三角形的性质即可得到结论.
解答 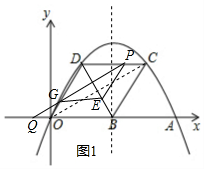 解:(1)把C(9,m)代入y=-$\frac{\sqrt{3}}{9}$x2+$\frac{4\sqrt{3}}{3}$x中得-$\frac{\sqrt{3}}{9}$×92+$\frac{4\sqrt{3}}{3}$×9=m,
解:(1)把C(9,m)代入y=-$\frac{\sqrt{3}}{9}$x2+$\frac{4\sqrt{3}}{3}$x中得-$\frac{\sqrt{3}}{9}$×92+$\frac{4\sqrt{3}}{3}$×9=m,
解得:m=3$\sqrt{3}$,
对称轴为:直线x=-$\frac{\frac{4\sqrt{3}}{3}}{2×(-\frac{\sqrt{3}}{9})}$=6,
故答案为:3$\sqrt{3}$,6;
(2)①如图1,连接OC,则OQ=t,DP=2t,
∵抛物线y=-$\frac{\sqrt{3}}{9}$x2+$\frac{4\sqrt{3}}{3}$x的对称轴是x=6,C(9,3$\sqrt{3}$),
∴D(3,3$\sqrt{3}$),OB=CD=6,
∵OB∥CD,
∴四边形OBCD是平行四边形,
∵OD=6,
∴OD=OB,
∴四边形OBCD是菱形,
∴OC⊥BD,
当E落在直线BD上时,PQ⊥BD,
∴PQ∥OC,
∴P在BC上时不存在符合条件的t值,P在DC上时,PC=6-2t,
∵PC∥AQ,且PQ∥OC,四边形PC OQ是平行四边形,
∴PC=OQ,
∴6-2t=t,解得:t=2,
∴当点E落在直线BD上时,t的值是2;
②当t=3.6时点E落在x轴上,
理由如下:设DE交PQ于F,PQ交OD于G,当P在DC上时,DP<DC,DG<DO,
则点E落在菱形OBCD内部,不可能落在x轴上,
如图2,当P在BC上时,PC=2t-6,PB═12-2t,由∠CBA=60°,
得P(12-t,$\sqrt{3}$(6-t)),Q(-t,0),
设直线PQ的解析式为y=kx+b,
解得直线PQ的解析式为y=$\frac{\sqrt{3}(6-t)}{12}$x+$\frac{\sqrt{3}(6-t)}{12}$,
若点E落在x轴上,设E(n,0),则点F是DE的中点,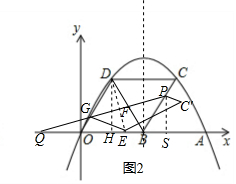
∵D(3,3$\sqrt{3}$),
∴F($\frac{3+n}{2}$,$\frac{3\sqrt{3}}{2}$),
∵点F在直线PQ上,
∴$\frac{3\sqrt{3}}{2}$=$\frac{\sqrt{3}(6-t)}{12}$×$\frac{3+n}{2}$+$\frac{\sqrt{3}(6-t)t}{12}$,
∵DE⊥PQ,过D作DH⊥OA于H过P作PS⊥OA于S,
得△PQS∽△EDH,
∴$\frac{PS}{QS}$=$\frac{EH}{DH}$,
∴$\frac{\sqrt{3}(6-t)}{12}$=$\frac{n-3}{3\sqrt{3}}$,
解得:t1=-6(不合题意,舍去),t2=3.6,
∴当t=3.6时点E落在x轴上.
点评 本题考查了求抛物线的对称轴,平行四边形的判定和性质,菱形的性质,函数与图形性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知线段a、b
如图:已知线段a、b查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 4 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |
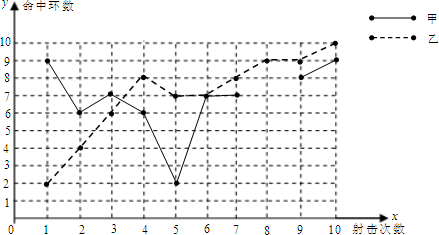
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
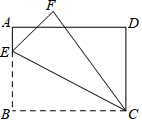 如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.
如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com