(1)证明:∵四边形ABCD和四边形AEFG是正方形,
∴AG=AE,AD=AB,∠GAE=∠BAD=90°,
∴∠GAE-∠DAE=∠DAB-∠DAE,
∴∠GAD=∠EAB,
在△ADG和△ABE中,
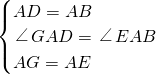
,
∴△ADG≌△ABE(SAS).
(2)证明:过F作FQ⊥BC于Q,
∵四边形ABCD、AEFG是正方形,
∴AB=BC,∠ABE=∠EQF=∠AEF=90°,AE=EF,
∴∠BAE+∠AEB=90°,∠AEB+∠FEQ=90°,
∴∠BAE=∠FEQ,
在△ABE和△EQF中,
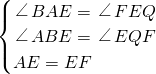
,
∴△ABE≌△EQF(AAS),
∴BE=FQ,AB=EQ=BC,
∴BC-EC=EQ-EC,
∴BE=CQ=FQ,
∵∠FQE=90°,
∴∠FCQ=∠CFQ=

(180°-90°)=45°.
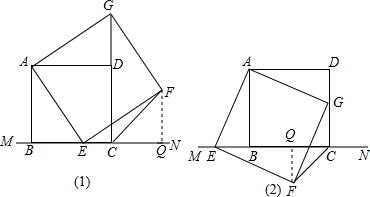
(3)解:∠FCN=135°,
理由是:过F作FQ⊥BC于Q,
∵四边形ABCD、AEFG是正方形,
∴AB=BC,∠ABE=∠EQF=∠AEF=90°,AE=EF,
∴∠BAE+∠AEB=90°,∠AEB+∠FEQ=90°,
∴∠BAE=∠FEQ,
在△ABE和△EQF中
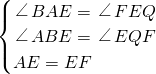
∴△ABE≌△EQF(AAS),
∴BE=FQ,AB=EQ=BC,
∴BC-BQ=EQ-BQ,
∴BE=CQ=FQ,
∵∠FQE=90°,
∴∠FCQ=∠CFQ=

(180°-90°)=45°,
∴∠FCN=180°-45°=135°.
分析:(1)根据正方形性质得出AG=AE,AD=AB,∠GAE=∠BAD=90°,求出∠GAD=∠EAB,根据SAS推出两三角形全等即可.
(2)过F作FQ⊥BC于Q,根据正方形的性质得出AB=BC,∠ABE=∠EQF=∠AEF=90°,AE=EF,求出∠BAE=∠FEQ,证△ABE≌△EQF,推出BE=FQ,AB=EQ=BC,求出BE=CQ=FQ,即可得出∠FCQ=∠CFQ=45°.
(3)过F作FQ⊥BC于Q,根据正方形的性质得出AB=BC,∠ABE=∠EQF=∠AEF=90°,AE=EF,求出∠BAE=∠FEQ,证△ABE≌△EQF,推出BE=FQ,AB=EQ=BC,求出BE=CQ=FQ,即可得出∠FCQ=∠CFQ=45°,即可求出答案.
点评:本题考查了全等三角形的性质和判定,三角形内角和定理,正方形性质的应用,主要考查学生的推理能力.

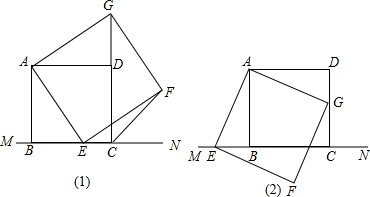
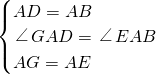 ,
,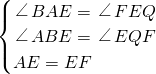 ,
, (180°-90°)=45°.
(180°-90°)=45°.
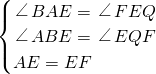
 (180°-90°)=45°,
(180°-90°)=45°,



 S1?
S1?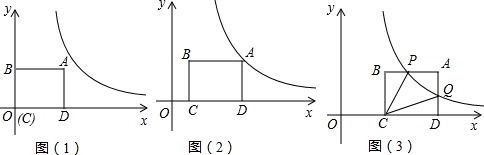
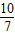 S1?
S1?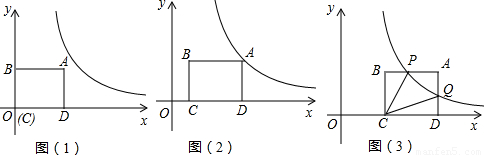
 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;