
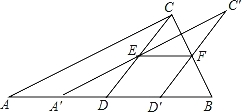
【题目】(2016湖北省荆州市第21题)如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
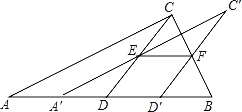
【答案】△A′DE是等腰三角形;证明过程见解析.
【解析】
试题分析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.
试题解析:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB, ∴CD=DA=DB, ∴∠DAC=∠DCA,
∵A′C∥AC, ∴∠DA′E=∠A,∠DEA′=∠DCA, ∴∠DA′E=∠DEA′, ∴DA′=DE,
∴△A′DE是等腰三角形. ∵四边形DEFD′是菱形, ∴EF=DE=DA′,EF∥DD′,
∴∠CEF=∠DA′E,∠EFC=∠CD′A′, ∵CD∥C′D′, ∴∠A′DE=∠A′D′C=∠EFC,
在△A′DE和△EFC′中,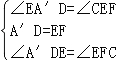 , ∴△A′DE≌△EFC′.
, ∴△A′DE≌△EFC′.


科目:初中数学 来源: 题型:
【题目】微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小,某种电子元件的面积大约为0.0000005平方毫米,用科学记数法表示为____平方毫米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一组对边平行且相等的四边形是平行四边形B.对角线相等的四边形是矩形
C.对角线相等的平行四边形是正方形D.对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
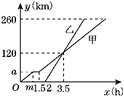
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com