
 以?ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.
以?ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.分析 (1)根据△AEB和△DGC是等腰直角三角形,得出AE=$\frac{\sqrt{2}}{2}$AB,DG=$\frac{\sqrt{2}}{2}$CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;
(2)与(1)证明过程类似求出GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,证△HAE≌△HDG,求出∠AHD=90°,∠EHG=90°,即可推出结论
解答 证明:(1)∵△AEB和△DGC是等腰直角三角形,
∴AE=$\frac{\sqrt{2}}{2}$AB,DG=$\frac{\sqrt{2}}{2}$CD,
在平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE,
∵△AHD是等腰直角三角形,
∴HA=HD,
∴△HAE≌△HDG,
∴HE=HG.
(2)由(1)同理可得:GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.
点评 本题主要考查对正方形的判定,等腰直角三角形的性质,菱形的判定和性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.


科目:初中数学 来源: 题型:填空题
 为全面推进“新两基”(基本普及15年教育及县域内义务教育基本均衡)工作,某县对辖区内的80所中小学上半年工作情况进行了专项督导考核,成绩分别记为A,B,C,D四等,绘制了扇形统计图(如图),则该县被考核的学校中得A等成绩的有56所.
为全面推进“新两基”(基本普及15年教育及县域内义务教育基本均衡)工作,某县对辖区内的80所中小学上半年工作情况进行了专项督导考核,成绩分别记为A,B,C,D四等,绘制了扇形统计图(如图),则该县被考核的学校中得A等成绩的有56所.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
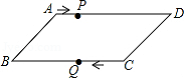 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.
如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若平行四边形ABCD的周长为42,FM=3,EF=4,则AB的长为( )
如图,平行四边形ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若平行四边形ABCD的周长为42,FM=3,EF=4,则AB的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com