
(12分)如图所示,E是正方形ABCD的边AB上的动点,正方形的边长为4, EF⊥DE交BC于点F.


(1)求证:△ADE ∽△BEF ;
(2)AE=x,BF=y.当x取什么值时,y有最大值? 并求出这个最大值;
(3)已知D、C 、F、E四点在同一个圆上,连接CE、DF,若sin∠CEF =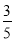 ,求此圆直径.
,求此圆直径.
(1)见解析;(2)当x=2时,y值最大,最大为1;(3)此圆直径为5.
【解析】
试题分析::(1)这两个三角形中,已知的条件有∠A=∠B=90°,那么只要得出另外两组对应角相等即可得出两三角形相似,因为∠DEA+∠FEB=180-90=90°,而∠ADE+∠DEA=90°,因此∠ADE=∠FEB,同理可得出∠BFE=∠AED,那么就构成了两三角形相似的条件;
(2)可用x表示出BE的长,然后根据(1)中三角形ADE和FEB相似可得出关于AD,AE,BE,BF的比例关系式,然后就能得出一个关于x,y的函数关系式.根据函数的性质即可得出y的最大值及相应的x的值.
(3)根据四点共圆,利用三角函数得出圆的直径.
试题解析:(1)证明:∵∠DEF=90°,
∴∠AED+∠BEF=90°,∠AED +∠ADE=90°,
∴∠ADE =∠BEF ,
∵∠A =∠B,
∴△ADE∽△BEF ;
(2)∵△ADE∽△BEF,
∴AD:BE=AE:BF,
∵AE=x,BF =y,AD =4,
∴4:x=(4-x):y,
∴y=-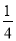 x2+x,
x2+x,
∴y=-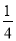 (x-2)2+1,
(x-2)2+1,
∴当x=2时,y值最大,最大为1;
∵D、C 、F、E四点共圆,
∴∠CEF=∠CDF,
∴sin∠CEF=sin∠CDF=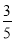 ,
,
∴DF=5,
即此圆直径为5
考点:正方形的性质;二次函数的最大值.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
某校八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,……请你根据①②步骤解答下列问题:
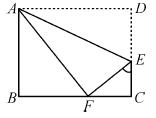
(1)找出图中∠FEC的余角;
(2)计算EC的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
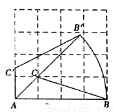
如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则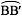 的长为( )
的长为( )
A. B.
B.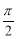 C.7
C.7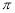 D.6
D.6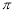
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知P是⊙O外一点,PA切⊙O于A,PB切⊙O于B.若PA=6,则PB= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
从l到9这九个自然数中任取一个,既是2的倍数又是3的倍数的概率是
A.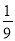 B.
B.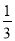 C.
C.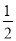 D.
D.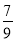
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在上,若PA长为2,则△PEF的周长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县七年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,∠AOB是直角,射线OC从OA出发,以每秒8度的速度顺时针方向转动;射线OD从OB出发,以每秒2度的速度逆时针方向转动.当OC与OA成一直线时停止转动.

(1)______秒时,OC与OD重合.
(2)当OC与OD的夹角是30度时,求转动的时间是多少秒?
(3)若OB平分∠COD,求转动的时间是多少秒?并画出此时的OC与OD,写出图中∠AOD的余角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com