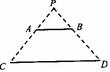
试题分析:(1) ①利用三角形的一个外角等于和它不相邻的两个内角的和,即可求证. ②利用两角相等的三角形相似.(2)利用前面所得的三角形相似,由对应边成比例,可求得x的值.(3)①根据旋转的性质,旋转前后的图形对应线段、对应角相等,可证得△ACP≌△BCP′,从而∠CAP=∠CBP′,然后根据等腰三角形的“三线合一”性质,得到∠CBP′=30°. ②根据“垂线段最短”这一定理,当∠BP′D=90°时,DP′最短.
试题解析:(1)①∵∠ADC=∠B+∠BAD, ∠ADC=∠ADG+∠CDG
∴∠B+∠BAD=∠ADG+∠CDG
∵三角形ABC是等边三角形
∴∠B=∠C=60°
∵∠ADG=60°
∴∠BAD=∠CDG
②由①知∠BAD=∠CDG
∵∠B=∠C
∴△ABD∽△DCG
(2)由(1)知△ABD∽△DCG,所以AB:CD=BD:CG,CD=6-x,AB=6,CG=

,BD=x,代入可求得:x=1或5.
(3) ①由旋转知∠PCP′=60°,CP=CP′,
∵△ABC是等边三角形
∴AC="BC," ∠ACB=60°
∴∠ACP=∠BCP′
∴△ACP≌△BCP′
∠CBP′=∠CAD=30°
②根据“垂线段最短”可知,当DP′⊥BP′时,DP′最短,此时,由于∠CBP′=30°,所以DP′=

BD=1.5.



 ,求x的值;
,求x的值;
 ,BD=x,代入可求得:x=1或5.
,BD=x,代入可求得:x=1或5. BD=1.5.
BD=1.5.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案