
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).
(1)求抛物线的解析式;
(2)点P从点O出发,乙每秒2个单位长度的速度向点B运动,同时点E也从点O出发,以每秒1个单位长度的速度向点C运动,设点P的运动时间t秒(0<t<2).
①过点E作x轴的平行线,与BC相交于点D(如图所示),当t为何值时, ![]() 的值最小,求出这个最小值并写出此时点E、P的坐标;
的值最小,求出这个最小值并写出此时点E、P的坐标;
②在满足①的条件下,抛物线的对称轴上是否存在点F,使△EFP为直角三角形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵y=ax2+bx+c(a≠0)与x轴交于A(2,0),B(4,0)两点,与y轴交于点C(0,2).
∴ 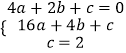 ,
,
解得: 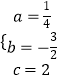
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+2.
x+2.
(2)
解:①由题意得:OP=2t,OE=t,
∵DE∥OB,
∴△CDE∽△CBO,
∴ ![]() ,即
,即 ![]() ,
,
∴DE=4﹣2t,
∴ ![]() ,
,
∵0<t<2,1﹣(t﹣1)2始终为正数,且t=1时,1﹣(t﹣1)2有最大值1,
∴t=1时, ![]() 有最小值1,即t=1时,
有最小值1,即t=1时, ![]() 有最小值1,此时OP=2,OE=1,
有最小值1,此时OP=2,OE=1,
∴E(0,1),P(2,0);
②存在,
∵抛物线y= ![]() x2﹣
x2﹣ ![]() x+2的对称轴方程为x=3,
x+2的对称轴方程为x=3,
设F(3,m),
∴EP2=5,PF2=(3﹣2)2+m2,EF2=(m﹣1)2+32,
当△EFP为直角三角形时,
(a)当∠EPF=90°时,
EP2+PF2=EF2,
即5+1+m2=(m﹣1)2+32,
解得:m=2,
(b)当∠EFP=90°时,
EF2+FP2=PE2,
即(m﹣1)2+32+(3﹣2)2+m2=5,
此方程无解,不合题意舍去,
∴当∠EFP=90°时,
这种情况不存在,
(c)当∠PEF=90°时,
EF2+PE2=PF2,
即(m﹣1)2+32+5=(3﹣2)2+m2,
解得:m=7,
∴F(3,2),(3,7).
【解析】(1)利用待定系数法求函数解析式即可;(2)①由题意得:OP=2t,OE=t,通过△CDE∽△CBO得到 ![]() ,即
,即 ![]() ,求得
,求得 ![]() 有最小值1,即可求得结果;②存在,求得抛物线y=
有最小值1,即可求得结果;②存在,求得抛物线y= ![]() x2﹣
x2﹣ ![]() x+2的对称方程为x=3,设F(3,m),当△EFP为直角三角形时(a)当∠EPF=90°时,(b)当∠EFP=90°时,(c)当∠PEF=90°时,根据勾股定理列方程即可求得结果.
x+2的对称方程为x=3,设F(3,m),当△EFP为直角三角形时(a)当∠EPF=90°时,(b)当∠EFP=90°时,(c)当∠PEF=90°时,根据勾股定理列方程即可求得结果.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,求:
(1)t分别为何值时,四边形PQCD为平行四边形、等腰梯形?
(2)t分别为何值时,直线PQ与⊙O相切、相离、相交?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,点E在正方形ABCD的边BC上,BF⊥AE于点F,DG⊥AE于点G,可知△ADG≌△BAF.(不要求证明)
拓展:如图②,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC,求证:△ABE≌△CAF.
应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.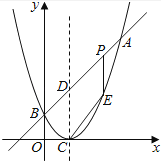
(1)求m的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程) 
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC与点G,连结AG、CF.则S△FCG为( ) 
A.3.6
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com