
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,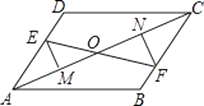
求证:
(1)EM=FN;
(2)EF与MN互相平分.
【答案】
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠EAM=∠FCN,
∵DE=BF,
∴AE=CF,∵EM⊥AC于M,FN⊥AC于N,∴∠AME=∠CNF=90°,
在△AEM和△CFN中,  ,
,
∴△AEM≌△CFN(AAS),
∴EM=FN
(2)证明:连接EN、FM,如图所示: 
∵EM⊥AC,FN⊥AC,
∴∠AME=∠EMN=∠FNC=∠FNM=90°,
∴EM∥FN,
又∵由(1)得EM=FN,
∴四边形EMFN是平行四边形,
∴EF与MN互相平分.
【解析】(1)根据平行四边形的性质得出AD∥BC,AD=BC,,进而得出∠EAM=∠FCN,根据等式的性质及垂直的定义知AE=CF,∠AME=∠CNF=90°,用AAS判断出△AEM≌△CFN,根据三角形全等的性质得出结论;
(2)连接EN、FM根据垂直于同一直线的两条直线互相平行得出EM∥FN,又EM=FN,利用平行四边形的判定方法判断出四边形EMFN是平行四边形,根据平行四边形的性质得出结论。


科目:初中数学 来源: 题型:
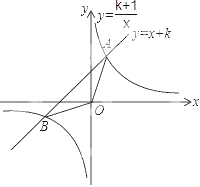
【题目】如图,已知直线![]() 和双曲线
和双曲线![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.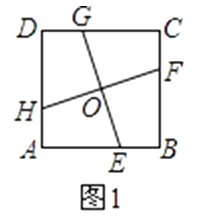
(1)如图1,连接GH,GF,求证:GH=GF;
(2)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(3)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2 . (直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解九年级500名学生的身体素质情况,体育老师对九年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示: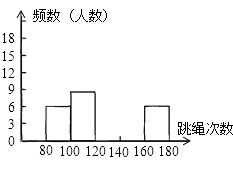
组别 | 次数x | 频数(人数) |
第l组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a=,次数在140≤x<160这组的频率为;
(2)请把频数分布直方图补充完整;
(3)若九年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,则这个年级合格的学生有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
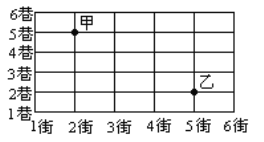
【题目】如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口,如果用(2,5)表示甲处的位置,那么“(2,5) ![]() (3,5)
(3,5) ![]() (4,5)
(4,5) ![]() (5,5)
(5,5) ![]() (5,4)
(5,4) ![]() (5,3)
(5,3) ![]() (5,2)”表示从甲处到乙处的一种路线.请你用有序数对写出几种从甲处到乙处的路线.
(5,2)”表示从甲处到乙处的一种路线.请你用有序数对写出几种从甲处到乙处的路线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com