
����Ŀ����ͼ1����������ABCD�У�E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA�ϵĵ㣬HA=EB=FC=GD������EG��FH������ΪO��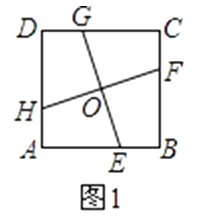
��1����ͼ1������GH��GF����֤��GH=GF��
��2����ͼ2������EF��FG��GH��HE�����ж��ı���EFGH����״����֤����Ľ��ۣ�
��3����������ABCD���߶�EG��HF�������ٰѵõ����ĸ��ı��ΰ�ͼ3�ķ�ʽƴ�ӳ�һ���ı��Σ���������ABCD�ı߳�Ϊ3cm��HA=EB=FC=GD=1cm����ͼ3����Ӱ���ֵ����Ϊcm2 �� ��ֱ��д�����
���𰸡�
��1��֤�������ı���EFGH�������Σ� ���C=��D=90�㣬AB=BC=CD=DA�� ��HA=EB=FC=GD��
��AE=BF=CG=DH�� ���CGF�ա�DHG �� GH=GF��
��2��֤�������ı���ABCD�������Σ�
���A=��B=��C=��D=90�㣬AB=BC=CD=DA��
��HA=EB=FC=GD��
��AE=BF=CG=DH��
���AEH�ա�BFE�ա�CGF�ա�DHG��
��EF=FG=GH=HE��
���ı���EFGH�����Σ�
�ߡ�DHG�ա�AEH��
���DHG=��AEH��
�ߡ�AEH+��AHE=90�㣬
���DHG+��AHE=90�㣬
���GHE=90�㣬
���ı���EFGH��������
��3���⣺S��Ӱ=1�� ��HA=EB=FC=GD=1��AB=BC=CD=AD=3�� ��GF=EF=EH=GH= ![]() ��
��
���ɣ�1��֪���ı���EFGH�������Σ� ��GO=OF����GOF=90�㣬 �ɹ��ɶ����ã�GO=OF= ![]() ��
��
��S�ı���FCGO= ![]() ��1��2+
��1��2+ ![]() ��
�� ![]() ��
�� ![]() =
= ![]() �� ��S��Ӱ=
�� ��S��Ӱ= ![]() ��S�ı���FCGO��4=10��9=1
��S�ı���FCGO��4=10��9=1
����������1�����������ε����ʵó���C=��D=90�㣬AB=BC=CD=DA�� �����֪�ó�AE=BF=CG=DH���Ӷ��жϳ���CGF�ա�DHG������ȫ�������ε����ʵó����ۣ�
��2�����������ε����ʵó���A=��B=��C=��D=90�㣬AB=BC=CD=DA�� �����֪�ó�AE=BF=CG=DH���Ӷ��Ƴ���AEH�ա�BFE�ա�CGF�ա�DHG����ȫ�������ε����ʵó�EF=FG=GH=HE�������жϳ��ı���EFGH�����Σ����ҳ���GHE=90�㣬���������ε��ж��ó��ı���EFGH�������Σ�
��3��������֪������֪������ƴ������ͼ���������Σ����ù��ɶ������GF,GO,FO�ij����Ӷ������Ӱ���ֵ������
�����㾫�������չ��ɶ����ĸ����ǽ����ĸ�������Ҫ֪��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ������ġ�һ��һ·�����轫�ٽ��ҹ�����������Ļ�����������һ��һ·�������������˿�ԼΪ4400000000�ˣ�������4400000000�ÿ�ѧ��������ʾΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����ҵı����У�������ʽ�ֽ������ ��
A. a��m+n��= am+an B. a2��b2��c2 =��a��b����a+b����c2
C. 10x2��5x = 5x��2x��1�� D. x2��16+6x =��x+4����x��4��+ 6x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������һ��p(x��y)��ƽ�ƺ��Ӧ��Ϊp1(x+5��y+3)������ABC��ͬ����ƽ�Ƶõ���A1B1C1.
��1��������A1B1C1��
��2����A1,B1,C1�����ꣻ
��3��д��ƽ�ƵĹ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��F�ֱ�Ϊƽ���ı���ABCD�ĶԱ�AD��BC�ϵĵ㣬��DE=BF��EM��AC��M��FN��AC��N��EF��AC�ڵ�O��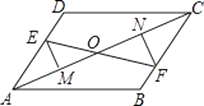
��֤��
��1��EM=FN��
��2��EF��MN����ƽ�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��˺��翪ʼʹ�ø������й��Ŵ���ѧ�����������������ġ����̡�һ�£���������ѧʷ���״���ʽ���븺�����������100Ԫ����+100Ԫ����ô��80Ԫ��ʾ�� ��
A.֧��20Ԫ
B.����20Ԫ
C.֧��80Ԫ
D.����80Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������14�֣���ͼ����A�Ͷ���P��ֱ��![]() �ϣ���P���ڵ�A�ĶԳƵ�ΪQ����AQΪ����Rt��ABQ��ʹ��BAQ=90����AQ:AB=3:4������ABQ�����ԲO����C�ڵ�P�Ҳ࣬PC=4������C��ֱ��
�ϣ���P���ڵ�A�ĶԳƵ�ΪQ����AQΪ����Rt��ABQ��ʹ��BAQ=90����AQ:AB=3:4������ABQ�����ԲO����C�ڵ�P�Ҳ࣬PC=4������C��ֱ��![]() ��
��![]() ������O��OD��
������O��OD��![]() �ڵ�D����AB�Ҳ��Բ���ڵ�E��������CD��ȡ��F��ʹDF=
�ڵ�D����AB�Ҳ��Բ���ڵ�E��������CD��ȡ��F��ʹDF=![]() CD����DE��DFΪ�ڱ�������DEGF����AQ=
CD����DE��DFΪ�ڱ�������DEGF����AQ=![]()
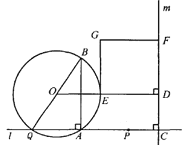
��1���ù���![]() �Ĵ���ʽ��ʾBQ��DF��
�Ĵ���ʽ��ʾBQ��DF��
��2������P�ڵ�A�Ҳ�ʱ��������DEGF���������90����AP�ij���
��3���ڵ�P�������˶������У�
����APΪ��ֵʱ������DEGF�������Σ�
����ֱ��BG����O����һ��N����BN�����ľ�Ϊ1����AP�ij���ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������ƽ������a������������8���ǣ� ��
A. a��8B. a��4C. a2��8D. a2��8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com