
分析 根据定义,将$\sum_{n=1}^{2016}$$\frac{1}{n(n+1)}$写成$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2016×2017}$后运用$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$化简计算可得结果.
解答 解:根据题意,知:
$\sum_{n=1}^{2016}$$\frac{1}{n(n+1)}$=$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2016×2017}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$,
故答案为:$\frac{2016}{2017}$
点评 本题主要考查新定义下分式的化简计算,根据对定义的理解准确列出算式是解题的前提,运用公式将分数拆开运算是解题的关键.


科目:初中数学 来源: 题型:选择题
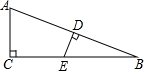 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
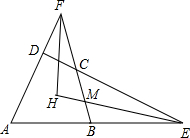 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com