
����Ŀ��Ϊ��ץס�����½���1000����̻���ij�̵��������A��B���������ڼ���Ʒ��������A�ּ���Ʒ8����B�ּ���Ʒ3������Ҫ950Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ6������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ����ô���̵깲�м��ֽ���������
���𰸡�
��1���⣺����̵깺��һ��A�ּ���Ʒ��ҪaԪ������һ��B�ּ���Ʒ��ҪbԪ��
��������÷�����ã� ![]() ��
��
�ⷽ����ã� ![]() ��
��
���һ��A�ּ���Ʒ��Ҫ100Ԫ������һ��B�ּ���Ʒ��Ҫ50Ԫ��
��2���⣺����̵깺��A�ּ���Ʒx������B�ּ���Ʒ�У�100��x������
�� ![]() ��
��
��ã�50��x��53��
��x ��������x=50��51��52��53
���4�ֽ���������
�ֱ�Ϊ������1���̵깺��A�ּ���Ʒ50������B�ּ���Ʒ��50����
����2���̵깺��A�ּ���Ʒ51������B�ּ���Ʒ��49����
����3���̵깺��A�ּ���Ʒ52������B�ּ���Ʒ��48����
����4���̵깺��A�ּ���Ʒ53������B�ּ���Ʒ��47����
����������1������̵깺��һ��A�ּ���Ʒ��ҪaԪ������һ��B�ּ���Ʒ��ҪbԪ��Ȼ������A�ּ���Ʒ8����ҪǮ��+B�ּ���Ʒ3��Ǯ��=950��A�ּ���Ʒ5����ҪǮ��+B�ּ���Ʒ6����ҪǮ��=800�з�������⼴�ɣ�
��2������̵깺��A�ּ���Ʒx������B�ּ���Ʒ�У�100��x������Ȼ�����ݹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ�в���ʽ����⼴��.
�����㾫��������һԪһ�β���ʽ���Ӧ�ö���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ƽ�����ǣ� ��
A.6�ı���
B.8�ı���
C.12�ı���
D.16�ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����BAC=90�㣬AD��BC������ΪD����������н��ۣ�
��AB��AC���ഹֱ
��AD��AC���ഹֱ
�۵�C��AB�Ĵ��߶����߶�AB
�ܵ�A��BC�ľ������߶�AD
���߶�AB�ij����ǵ�B��AC�ľ���
���߶�AB�ǵ�B��AC�ľ��룮
������ȷ���У�������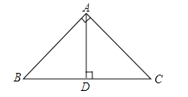
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ��Բ���о��ʹ��������Ӧ���õĺ��ʵĵ��鷽ʽΪ________________��(ѡ����ȫ���������������������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������棺��¿��װ30����ÿ���ۼ�300Ԫ����һ���Թ�����10��ʱ���ۼ۲��䣻��һ���Թ���10��ʱ��ÿ����1���������ÿ����װ���ۼ۾�����3Ԫ����֪�÷�װ�ɱ���ÿ��200Ԫ����˿�һ���Թ����װx��ʱ����������л���yԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2���˿�һ���Թ�����ټ�ʱ����������л�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC��������������ΪA����3��4����B����4��2����C����2��1������ABC��ԭ����ʱ����ת90�㣬�õ���A1B1C1����A1B1C1����ƽ��6����λ��������ƽ��2����λ�õ���A2B2C2��
��1��������A1B1Cl�͡�A2B2C2��
��2��P��a��b���ǡ�ABC��AC����һ�㣬��ABC����ת��ƽ�ƺ��P�Ķ�Ӧ��ֱ�ΪP1��P2����д����P1��P2�����꣮
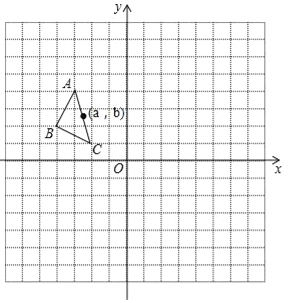
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com