练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，∠BAC=90°，AD⊥BC，垂足为D，则给出下列结论：
    ①AB与AC互相垂直
    ②AD与AC互相垂直
    ③点C到AB的垂线段是线段AB
    ④点A到BC的距离是线段AD
    ⑤线段AB的长度是点B到AC的距离
    ⑥线段AB是点B到AC的距离．
    其中正确的有（　　）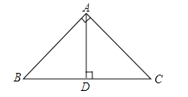

    A.2个
    B.3个
    C.4个
    D.5个

    【答案】A
    【解析】解：①AB与AC互相垂直，说法正确；
    ②AD与AC互相垂直，说法错误；
    ③点C到AB的垂线段是线段AB，说法错误；
    ④点A到BC的距离是线段AD，说法错误；
    ⑤线段AB的长度是点B到AC的距离，说法正确；
    ⑥线段AB是点B到AC的距离，说法错误；
    故选：A．
    根据垂线定义可得①正确，②错误；根据垂线段的定义可得③④错误；根据点到直线的距离可得⑤正确，⑥错误．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算：2﹣3= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】底面半径为10cm，高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm，高为5cm的圆柱形杯子，如果剩下的水倒在长、宽、高分别为50cm，20cm和12cm的长方体容器内，会满出来吗？若没有满出来，求出长方体容器内水的高度（ 取3）。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线与x轴交于点A（﹣5，0）、B（﹣1，0），与y轴交于点C（0，﹣5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．

    （1）求该抛物线所对应的函数解析式；

    （2）若点P的坐标为（﹣2，3），请求出此时△APC的面积；

    （3）过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．

    ①若∠APE=∠CPE，求证：；

    ②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由．

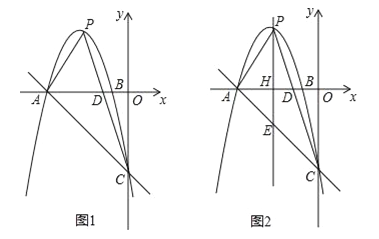
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2开始，连续的偶数相加，它们和的情况如下表：

    （1）如果n =8时，那么S的值为；
    （2）根据表中的规律猜想：用n的代数式表示S的公式为S=2+4+6+8+…+2n =；
    （3）根据上题的规律计算102+104+106+…+2006的值(要有计算过程).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系xOy中，抛物线经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．

    （1）求抛物线的解析式，并写出其顶点B的坐标；

    （2）①当P点运动到A点处时，计算：PO= ，PH= ，由此发现，PO PH（填“＞”、“＜”或“=”）；

    ②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；

    （3）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．

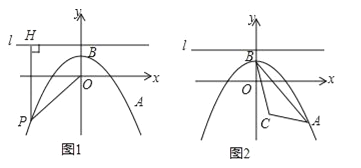
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】福建省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动，某中学为了了解本校学生的上学方式，在全校范围内随机抽查了部分学生，将收集的数据绘制成如下两幅不完整的统计图（如图所示），请根据图中提供的信息，解答下列问题．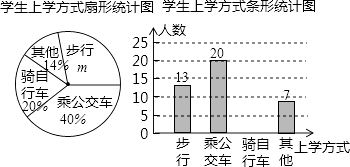

    （1）m=%，这次共抽取名学生进行调查；并补全条形图；
    （2）在这次抽样调查中，采用哪种上学方式的人数最多？
    （3）如果该校共有6000名学生，请你估计该校骑自行车上学的学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住保国寺建寺1000年的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．
    （1）求购进A、B两种纪念品每件各需多少元？
    （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4，则四边形ACEB的周长为 ．

    查看答案和解析>>

    同步练习册答案