
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程).
【答案】
(1)72
(2)n(n+1)
(3)解:原式=(2+4+6+…+2006)﹣(2+4+6+…+100)
=1003×1004﹣50×51=1007012﹣2550
=1004462.
【解析】(1)根据已知从2开始,连续的偶数相加,观察表中的规律:1个偶数是2,,2个连续偶数的和为2![]() (1+2),3个连续偶数和为3
(1+2),3个连续偶数和为3![]() (1+3)
(1+3)![]() 8个连续偶数的和为8
8个连续偶数的和为8![]() 9=72.
9=72.
(2)S=2+4+6+8+…+2n =![]() n(2+2n)=n(n+1)。
n(2+2n)=n(n+1)。
(3)观察所求的式子,要求102+104+106+…+2006的值转化为求(2+4+6+…+2006)﹣(2+4+6+…+100)的值,根据(2)中得出的规律即可求解。
【考点精析】通过灵活运用数与式的规律和有理数的四则混合运算,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律;在没有括号的不同级运算中,先算乘方再算乘除,最后算加减即可以解答此题.


科目:初中数学 来源: 题型:
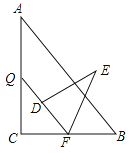
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:![]() 相交于A,B两点(点B在第一象限),点D在AB的延长线上.
相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=![]() AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求![]() 的值,并直接写出
的值,并直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:
①AB与AC互相垂直
②AD与AC互相垂直
③点C到AB的垂线段是线段AB
④点A到BC的距离是线段AD
⑤线段AB的长度是点B到AC的距离
⑥线段AB是点B到AC的距离.
其中正确的有( )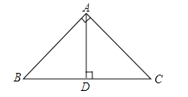
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
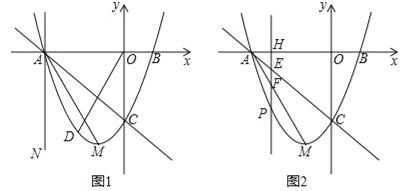
【题目】在平面直角坐标系中,已知抛物线![]() 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线x=t与x轴相交于点H.
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为![]() ,求此时t的值.
,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
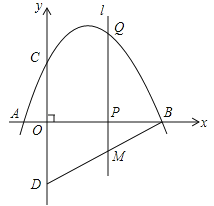
【题目】如图,抛物线![]() 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com