
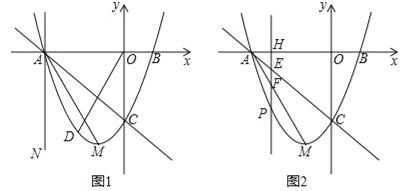
【题目】在平面直角坐标系中,已知抛物线![]() 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线x=t与x轴相交于点H.
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为![]() ,求此时t的值.
,求此时t的值.
【答案】(1)2,﹣3,y=﹣x﹣3;(2)①D(![]() ,
,![]() );②t=
);②t=![]() .
.
【解析】
试题分析:(1)根据顶点坐标列出关于b、c的方程组求解可得,由抛物线解析式求得A、C坐标,利用待定系数法可得直线AC解析式;
(2)①设点D的坐标为(m,![]() ),由∠COD=∠MAN得tan∠COD=tan∠MAN,列出关于m的方程求解可得;②求出直线AM的解析式,进而可用含t的式子表示出HE、EF、FP的长度,根据等腰三角形定义即可判定;由等腰三角形底角的余弦值为
),由∠COD=∠MAN得tan∠COD=tan∠MAN,列出关于m的方程求解可得;②求出直线AM的解析式,进而可用含t的式子表示出HE、EF、FP的长度,根据等腰三角形定义即可判定;由等腰三角形底角的余弦值为![]() 可得
可得![]() =
=![]() ,列方程可求得t的值.
,列方程可求得t的值.
试题解析:(1)∵抛物线![]() 的顶点M的坐标为(﹣1,﹣4),∴
的顶点M的坐标为(﹣1,﹣4),∴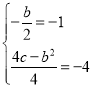 ,解得:
,解得:![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ,令y=0,得:
,令y=0,得:![]() ,解得:
,解得:![]() ,
,![]() ,∴A(﹣3,0),B(1,0),令x=0,得y=﹣3,∴C(0,﹣3),设直线AC的解析式为:y=kx+b,将A(﹣3,0),C(0,﹣3)代入,得:
,∴A(﹣3,0),B(1,0),令x=0,得y=﹣3,∴C(0,﹣3),设直线AC的解析式为:y=kx+b,将A(﹣3,0),C(0,﹣3)代入,得:![]() ,解得:
,解得:![]() ,∴直线AC的解析式为:y=﹣x﹣3;故答案为:2,﹣3,y=﹣x﹣3.
,∴直线AC的解析式为:y=﹣x﹣3;故答案为:2,﹣3,y=﹣x﹣3.
(2)①设点D的坐标为(m,![]() ),∵∠COD=∠MAN,∴tan∠COD=tan∠MAN,∴
),∵∠COD=∠MAN,∴tan∠COD=tan∠MAN,∴![]() ,解得:m=
,解得:m=![]() ,∵﹣3<m<0,∴m=
,∵﹣3<m<0,∴m=![]() ,故点D的坐标为(
,故点D的坐标为(![]() ,
,![]() );
);
②设直线AM的解析式为y=mx+n,将点A(﹣3,0)、M(﹣1,﹣4)代入,得:![]() ,解得:
,解得:![]() ,∴直线AM的解析式为:y=﹣2x﹣6,∵当x=t时,HE=﹣(﹣t﹣3)=t+3,HF=﹣(﹣2t﹣6)=2t+6,HP=
,∴直线AM的解析式为:y=﹣2x﹣6,∵当x=t时,HE=﹣(﹣t﹣3)=t+3,HF=﹣(﹣2t﹣6)=2t+6,HP=![]() ,∴HE=EF=HF﹣HE=t+3,FP=
,∴HE=EF=HF﹣HE=t+3,FP=![]() ,∵HE+EF﹣FP=
,∵HE+EF﹣FP=![]() =
=![]() >0,∴HE+EF>FP,又HE+FP>EF,EF+FP>HE,∴当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形;
>0,∴HE+EF>FP,又HE+FP>EF,EF+FP>HE,∴当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形;
由题意得:![]() =
=![]() ,即
,即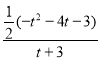 =
=![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,
, ![]() ,∵﹣3<t<﹣1,∴t=
,∵﹣3<t<﹣1,∴t=![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
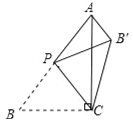
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=![]() ;
;
④B′A长度的最小值是1.
其中正确的判断是 (填入正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上. 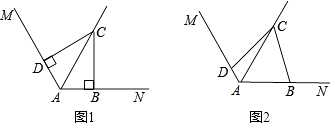
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福建省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.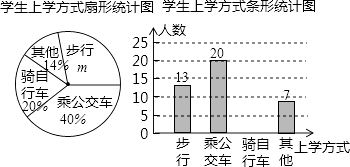
(1)m=%,这次共抽取名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有6000名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各数: ![]() ,3.1415,
,3.1415, ![]() ,0,
,0, ![]() ,
, ![]() ,1.3030030003……(每两个3之间多一个0)中,
,1.3030030003……(每两个3之间多一个0)中,
(1)无理数为:;
(2)整数为:;
(3)按从小到大排列,并用“<”连接.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com