
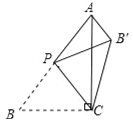
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则下列判断:
①当AP=BP时,AB′∥CP;
②当AP=BP时,∠B′PC=2∠B′AC
③当CP⊥AB时,AP=![]() ;
;
④B′A长度的最小值是1.
其中正确的判断是 (填入正确结论的序号)
【答案】①②④.
【解析】
试题分析:①∵在△ABC中,∠ACB=90°,AP=BP,∴AP=BP=CP,∴∠B=∠BPC=![]() (180°﹣∠APB′),由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=
(180°﹣∠APB′),由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=![]() (180°﹣∠APB′),∴AP=B′P,∴∠AB′P=′B′AP=
(180°﹣∠APB′),∴AP=B′P,∴∠AB′P=′B′AP=![]() (180°﹣∠APB′),∴∠AB′P=∠CPB′,∴AB′∥CP;故①正确;
(180°﹣∠APB′),∴∠AB′P=∠CPB′,∴AB′∥CP;故①正确;
②∵AP=BP,∴PA=PB′=PC=PB,∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,∵由折叠的性质可得:BC=B′C,∴![]() ,∴∠B′PC=2∠B′AC;故②正确;
,∴∠B′PC=2∠B′AC;故②正确;
③当CP⊥AB时,∠APC=∠ACB,∵∠PAC=∠CAB,∴△ACP∽△ABC,∴![]() ,∵在Rt△ABC中,由勾股定理可知:AC=
,∵在Rt△ABC中,由勾股定理可知:AC=![]() =
=![]() =4,∴AP=
=4,∴AP=![]() =
=![]() ;故③错误;
;故③错误;
④由轴对称的性质可知:BC=CB′=3,∵CB′长度固定不变,∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A.B′、C三点在一条直线上时,AB′有最小值,∴AB′=AC﹣B′C=4﹣3=1.故④正确.
故答案为:①②④.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( ) 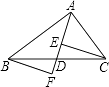
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定满足( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线相等且相互平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() 的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b= ,c= ,直线AC的解析式为 ;
(2)直线x=t与x轴相交于点H.
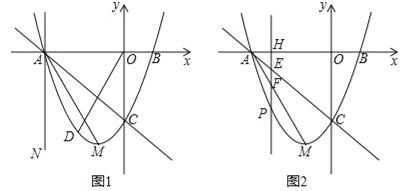
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为![]() ,求此时t的值.
,求此时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com