
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为 . 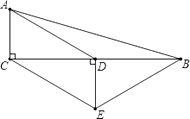
【答案】10+2 ![]()
【解析】解:∵∠ACB=90°,DE⊥BC, ∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,
∴BC=2CD=4 ![]() ,
,
在△ABC中,∠ACB=90°,
由勾股定理得AB= ![]() =2
=2 ![]() ,
,
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2 ![]() ,
,
所以答案是:10+2 ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和三角形中位线定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:
①AB与AC互相垂直
②AD与AC互相垂直
③点C到AB的垂线段是线段AB
④点A到BC的距离是线段AD
⑤线段AB的长度是点B到AC的距离
⑥线段AB是点B到AC的距离.
其中正确的有( )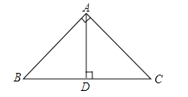
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
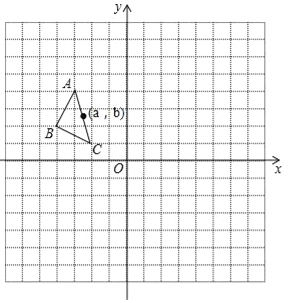
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
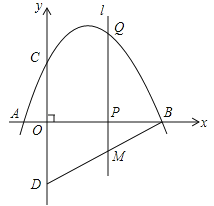
【题目】如图,抛物线![]() 与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A、点B、点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
特别说明:毛利润=售价﹣进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为1080元.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2 ).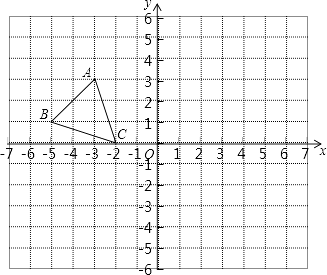
(1)直接写出点A1 , B1 , C1的坐标.
(2)在图中画出△A1B1C1 .
(3)连接A A1 , 求△AOA1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com