
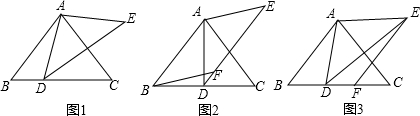
分析 (1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
解答 解:(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°-2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°-α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°-α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
点评 此题考查了平行四边形的判定与性质以及等腰三角形的性质与判定.注意(2)①中证得AD⊥BC是关键,(2)②中证得AD=CD是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | AB=DC | B. | AC=BD | C. | AB=DC且AC=BD | D. | AC⊥BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 45元 | B. | 50元 | C. | 55元 | D. | 60元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
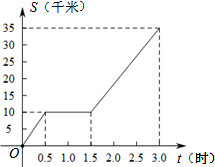 一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )| A. | 20千米/时 | B. | $\frac{35}{3}$千米/时 | C. | 10千米/时 | D. | $\frac{50}{3}$千米/时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
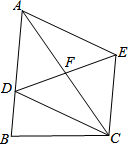 如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.
如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 3.284×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
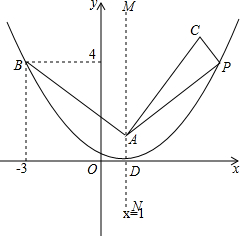 如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.
如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com