
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:2012届湖南省临武县楚江中学初中毕业学业考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴 与
与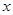 轴相交于点M.
轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)设点P为抛物线( )上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
正整数,请你直接写出点P的坐标;
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求
出点N的坐标;若不存在,请你说明理由. 
查看答案和解析>>
科目:初中数学 来源:2013年江苏省南京市鼓楼区中考一模数学试卷(解析版) 题型:解答题
【问题提出】
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
【初步思考】
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
【深入探究】
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;
Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;
Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图, .
求证: .
证明:

(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形 和四边形
和四边形 为例,分为以下四类:
为例,分为以下四类:
① ,
, ,
, ,
,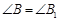 ,
, ;
;
② ,
, ,
, ,
,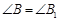 ,
,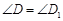 ;
;
③ ,
, ,
,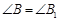 ,
, ,
,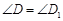 ;
;
④ ,
, ,
, ,
,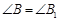 ,
, ;
;
其中能判定四边形 和四边形
和四边形 全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com