
矩形纸片ABCD的边长AB=8,AD=4,将矩形纸片沿EF折叠,使点A与点C重合,折叠后在某一面着色(如图),则着色部分的面积为( )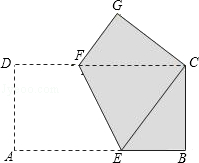
| A.16 | B.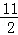 | C.22 | D.8 |
C
解析试题分析:根据折叠的性质可知着色部分的面积等于S矩形ABCD﹣S△CEF,应先利用勾股定理求得FC的长,进而求得△CEF的面积,代入求值即可.
解:由折叠的性质可得:CG=AD=4,GF=DF=CD﹣CF,∠G=90°,
则△CFG为直角三角形,
在Rt△CFG中,FC2﹣CG2=FG2,
即FC2﹣42=(8﹣FC)2,
解得:FC=5,
∴S△CEF=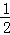 FC•AD=
FC•AD=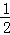 ×5×4=10,
×5×4=10,
则着色部分的面积为:S矩形ABCD﹣S△CEF=AB•AD﹣10=8×4﹣10=22.
故选C.
点评:本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,由折叠得到相等的边,相等的角,并利用勾股定理求解,要求同学们熟练掌握矩形和三角形的面积公式以及图形面积的转换.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源:东北师大版(2014) 七年级下 题型:
| |||||||||||||||
查看答案和解析>>
科目:初中数学 来源:2015届初中数学苏教版八年级上册第六章练习卷(解析版) 题型:选择题
在一次射击练习中,某运动员命中的环数是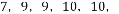 其中
其中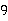 是( )
是( )
A.平均数 B.中位数
C.众数 D.既是平均数又是中位数、众数
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com