【题目】如图,函数
和
(
是常数,且
)在同一平面直角坐标系的图象可能是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
可先根据一次函数的图象判断a的符号，再判断二次函数图象与实际是否相符，判断正误即可．
A．由一次函数y=ax﹣a的图象可得：a＜0，此时二次函数y=ax2﹣2x+1的图象应该开口向下．故选项错误；
B．由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上，对称轴x=﹣
＞0．故选项正确；
C．由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上，对称轴x=﹣＞0，和x轴的正半轴相交．故选项错误；
D．由一次函数y=ax﹣a的图象可得：a＞0，此时二次函数y=ax2﹣2x+1的图象应该开口向上．故选项错误．
故选B．
科目：初中数学 来源： 题型：
【题目】如图，已知
，按如下步骤作图：
①分别以
、
为圆心，以大于
的长为半径在
两边作弧，交于两点
、
；
②作直线
，分别交
、于点
、
；
③过作
交于点
，连接
、
．
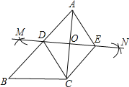
求证：四边形
是菱形；
当
，
，
，求四边形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，A（﹣1，5）、B（﹣1，0）、C（﹣4，3）．
（1）请画出△ABC关于y轴对称的△DEF（其中D、E、F分别是A、B、C的对应点）．
（2）直接写出（1）中F点的坐标为 ．
（3）若直线l经过点（0，﹣2）且与x轴平行，则点C关于直线l的对称点的坐标为 ．
（4）在y轴上存在一点P，使PC﹣PB最大，则点P的坐标为 ．
（5）第一象限有一点M（4，2），在x轴上找一点Q使CQ+MQ最短，画出最短路径，保留作图痕迹．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，每个小正方形的边长为1，点A的坐标为（-3，2）.请按要求分别完成下列各小题：
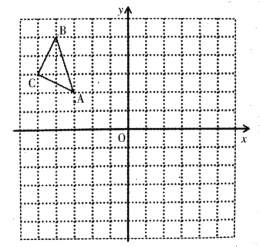
（1）把△ABC向下平移4个单位得到△A1B1C1，画出△A1B1C1，点A1的坐标是___.
（2）画出△ABC关于y轴对称的△A2B2C2，则点C2的坐标是 ；
（3）△ABC的面积是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某批乒乓球的质量检验结果如下：
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于
， 问至少取出了多少个黑球？
查看答案和解析>>
科目：初中数学 来源： 题型：
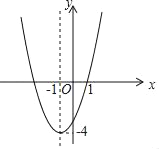
【题目】已知二次函数的图象如图所示．
（1）求这个二次函数的表达式；
（2）将该二次函数图象向上平移 个单位长度后恰好过点（﹣2，0）；
（3）观察图象，当﹣2＜x＜1时，y的取值范围为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：二次函数y=﹣2x2+4x+m+1，与x轴的公共点为A，B．
（1）如果A与B重合，求m的值；
（2）横、纵坐标都是整数的点叫做整点：
①当m=﹣1时，求线段AB上整点的个数；
②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n≤8时，结合函数的图象，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边△ABC中，点E为边AB上任意一点，点D在边CB的延长线上，且ED＝EC.
(1)当点E为AB的中点时(如图1)，则有AE DB(填“＞”“＜”或“＝”)；
(2)猜想AE与DB的数量关系，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．
探究展示：勤奋小组发现，AM垂直平分DE，并展示了如下的证明方法：
证明：∵BE=AB，∴AE=2AB．
∵AD=2AB，∴AD=AE．
∵四边形ABCD是矩形，∴AD∥BC．
∴
．（依据1）
∵BE=AB，∴
．∴EM=DM．
即AM是△ADE的DE边上的中线，
又∵AD=AE，∴AM⊥DE．（依据2）
∴AM垂直平分DE．
反思交流：
（1）①上述证明过程中的“依据1”“依据2”分别是指什么？
②试判断图1中的点A是否在线段GF的垂直平分线上，请直接回答，不必证明；
（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；
探索发现：
（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，可以发现点C，点B都在线段AE的垂直平分线上，除此之外，请观察矩形ABCD和正方形CEFG的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
