练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（　　）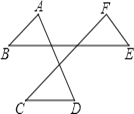

    A.180°
    B.360°
    C.540°
    D.720°

    【答案】B
    【解析】如图，

    ∵∠GKH=180°-（∠A+∠B），
    ∠HGK=180°-（∠C+∠D），
    ∠KHG=180°-（∠E+∠F），
    且∠GKH+∠HGK +∠KHG=180°，
    ∴3×180°-（∠A+∠B+∠C+∠D+∠E+∠F）=180°，
    ∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
    【考点精析】认真审题，首先需要了解三角形的内角和外角(三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，则∠A+∠B+∠C+∠D+∠E=（　　）度

    A.90
    B.180
    C.200
    D.360

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式与2x－(－3y－4z)相等的是( )

    A. 2x＋(－3y＋4z) B. 2x＋(3y＋4z)

    C. 2x＋(3y－4z) D. 2x＋(－3y－4z)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AD∥BC，∠ADC=α，P为直线CD上一动点，点M在线段BC上，连MP，∠MPD=β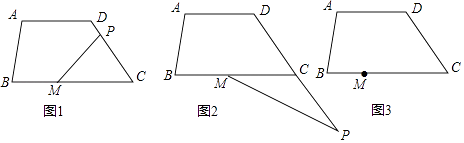
    （1）如图，若MP⊥CD，α=120°，则∠BMP=；
    （2）如图，当P点在DC延长线上时，∠BMP=；
    （3）如图，当P点在CD延长线上时，请画出图形，写出∠BMP、β、α之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC和△A′B′C′中，∠A=60°，∠B=40°，∠A’=60°，当∠C′= 时，△ABC∽△A′B′C′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为(1，0)，点D的坐标为(-3，0)，点B的坐标为(0，4)，已知点E(m，0)是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

    (1)求该抛物线的解析式；

    (2)当点P在直线BC上方时，请用含m的代数式表示PG的长度；

    (3)在(2)的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

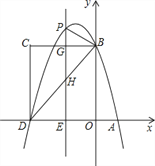
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求解：如图，在△ABC中，∠A=42°，∠ABC和∠ACB的平分线相交于点D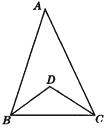

    （1）求∠BDC的度数．
    （2）在（1）中去掉∠A=42°这个条件，请探究∠BDC和∠A之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣2（x+1）2﹣2的顶点坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1+∠2﹦180°，∠3﹦∠B，则DE∥BC，下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容． 证明：
    ∵∠1+∠2﹦180（已知），
    ∠1﹦∠4 （），
    ∴∠2﹢﹦180°．
    ∴EH∥AB （）．
    ∴∠B﹦∠EHC（）．
    ∵∠3﹦∠B（已知）
    ∴∠3﹦∠EHC（）．
    ∴DE∥BC（）．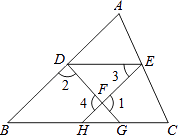

    查看答案和解析>>

    同步练习册答案