
 如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AB=16cm,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.分析 (1)由AAS证明△ADF≌△ADM,得出AM=AF=10cm;由角平分线的性质得出DF=DM,得出S△ABD:S△ACD=AB:AC,即可得出答案;
(2)由于DF=DM,所以S△AED与S△DGC之比就等于AE与CG之比,而AE与CG之比为2;
(3)只需让EF=MG即可;
(4)由$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$=$\frac{8}{7}$,即可得出答案.
解答 解:(1)∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴∠AFD=∠AMD=90°,DF=DM,
在△ADF和△ADM中,$\left\{\begin{array}{l}{∠BAD=∠DAC}&{\;}\\{∠AFD=∠AMD}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△ADF≌△ADM(AAS),
∴AM=AF=10cm;
∵S△ABD=$\frac{1}{2}$AB•DF,S△ACD=$\frac{1}{2}$AC•DM,
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB}{AC}$=$\frac{16}{14}$=$\frac{8}{7}$;
故答案为:10,$\frac{8}{7}$;
(2)∵S△AED=$\frac{1}{2}$AE•DF,S△DGC=$\frac{1}{2}$CG•DM,
∴$\frac{{S}_{△AED}}{{S}_{△DGC}}$=$\frac{AE}{CG}$,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2t,CG=t.
∴∴$\frac{{S}_{△AED}}{{S}_{△DGC}}$=$\frac{AE}{CG}$=2,
∴在运动过程中,不管t取何值,都有S△AED=2S△DGC;
(3)∵∠BAD=∠DAC,AD=AD,DF=DM,
∴△ADF≌△ADM.
∴AF=AM=10.
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,运动时间为t,
∴EF=AF-AE=10-2t,CG=t.
∴0<t<5.
①当M在线段CG上时,MG=CG-(AC-AM)=t-4.
当EF=MG时△DFE与△DMG全等时.
∴10-2t=t-4.
解得:t=$\frac{14}{3}$.
②当M在线段CG延长线上时,MG=4-t.
∴10-2t=4-t.
解得t=6(舍去).
③当E在BF上时,2t-10=t-4,
解得:t=6,符合题意,
∴当 t=$\frac{14}{3}$s或6s时,△DFE 与△DMG 全等.
(4)∵$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{8}{7}$,
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$=$\frac{8}{7}$,
∵BD=8,
∴CD=7,
故答案为:7.
点评 本题是三角形综合题目,考查了角平分线的性质、三角形面积的计算、全等三角形的判定与性质等知识点,难度适中.


科目:初中数学 来源: 题型:填空题
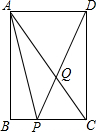 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
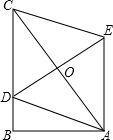 如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )
如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是( )| A. | 5 | B. | 6 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
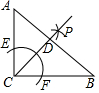 如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:
如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
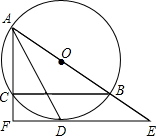 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
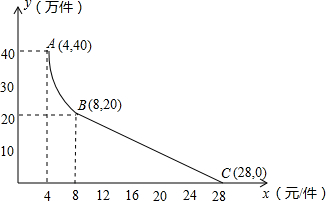 月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 第一天7:00-8:00 | 第二天7:00-8:00 | 第三天7:00-8:00 | 第四天7:00-8:00 | 第五天7:00-8:00 |
| 需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com