
 如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.
如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2. 分析 分别延长AE、BF交于点H,易证四边形EPFH为平行四边形,得出M为PH中点,则M的运行轨迹为三角形HCD的中位线GN.再求出CD的长,运用中位线的性质求出GN的长度即可.
解答 解:如图,分别延长AE、BF交于点H,
∵∠A=∠FPB=60°,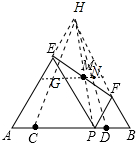
∴AH∥PF,
∵∠B=∠EPA=60°,
∴BH∥PE,
∴四边形EPFH为平行四边形,
∴EF与HP互相平分.
∵M为EF的中点,
∴M正好为PH中点,即在P的运动过程中,M始终为PH的中点,所以M的运行轨迹为三角形HCD的中位线GN.
∵CD=6-1-1=4,
∴GN=$\frac{1}{2}$CD=2,即M的移动路径长为2.
故答案为:2.
点评 本题考查了三角形中位线定理及等边三角形的性质,解答本题的关键是作出辅助线,找到点M移动的规律,判断出其运动路径,综合性较强.


科目:初中数学 来源: 题型:选择题
| A. | 点B | B. | 点C | C. | 点D | D. | 点E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
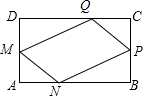 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 知识问卷得分(单位:分) | 65 | 70 | 75 | 80 | 85 |
| 人数 | 1 | 15 | 15 | 16 | 3 |
| A. | 15 | B. | 16 | C. | 80 | D. | 72.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;
(1)计算:|-2|-$\sqrt{9}$+(-$\frac{1}{2}$)-1;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为5.5秒或14.5秒.
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为5.5秒或14.5秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )
如图,在平面直角坐标系中,已知点A(2,0),B(0,3),如果将线段AB绕点B顺时针旋转90°至CB,那么点C的坐标是( )| A. | (-3,2) | B. | (-3,1) | C. | (2,1) | D. | (-2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com