
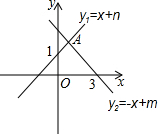 如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1.
如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1. 分析 先利用待定系数法分别求出m与n的值,再求出点A的横坐标,观察图象即可得出不等式x+n≥-x+m的解集.
解答 解:∵直线y1=x+n与y轴交于点(0,1),
∴1=0+n,解得n=1.
∵直线y2=-x+m与x轴交于点(3,0),
∴-3+m=0,解得m=3.
∵直线y1=x+1与直线y2=-x+3交于点A,
∴x+1=-x+3,解得x=1,
∴点A的横坐标是x=1,
∴不等式x+n≥-x+m的解集为x≥1.
故答案为x≥1.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.也考查了待定系数法求一次函数的解析式.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号)
如图,在矩形ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,有列结论:①AF=AE ②EF=2$\sqrt{5}$③AF=EF④S△AEF=10,其中正确的结论有①②④.(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
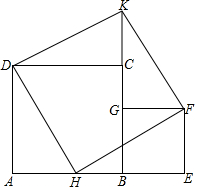 在线段AE上取一点B使AB>BE,以AB、BE为边在AE同侧作正方形ABCD、BEFG,在AB上取AH=BE在BC的延长线上取K使CK=BE,联结DK、KF、DH、HF
在线段AE上取一点B使AB>BE,以AB、BE为边在AE同侧作正方形ABCD、BEFG,在AB上取AH=BE在BC的延长线上取K使CK=BE,联结DK、KF、DH、HF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?
如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com