
 如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?
如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少? 分析 直接利用直角三角形中30°所对边等于斜边的一半,得出DB的长,进而利用勾股定理得出AB,AC,BC的长,再利用三角形面积求法得出答案.
解答 解:∵∠ABD=90°,∠DAB=30°,AD=80cm,
∴BD=40cm,
∴AB=$\sqrt{8{0}^{2}-4{0}^{2}}$=40$\sqrt{3}$(cm),
∵∠ACB=90°,CA=CB,
∴设AC=BC=xcm,
则2x2=(40$\sqrt{3}$)2,
解得:x=20$\sqrt{6}$,
则S△ACB=$\frac{1}{2}$x2=1200(cm2),
S△ABD=$\frac{1}{2}$×AB×BD=$\frac{1}{2}$×40×40$\sqrt{3}$=800$\sqrt{3}$(cm2),
故这块菜地的面积是:(1200+800$\sqrt{3}$)cm2.
点评 此题主要考查了勾股定理的应用以及三角形面积求法,正确得出三角形各边长是解题关键.


科目:初中数学 来源: 题型:填空题
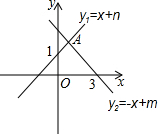 如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1.
如图所示,直线y1=x+n与y轴交于点(0,1),直线y2=-x+m与x轴交于点(3,0),两直线交于点A.不等式x+n≥-x+m的解集为x≥1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=60°,则∠EGC的度数为60°.
已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′,EB′分别交边AC于点F,G,若∠ADF=60°,则∠EGC的度数为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com