

分析 ①利用三角形的面积公式得出函数关系式,利用二次函数的极值的确定方法得出最大值;
②借助知识拓展,由S△AOC=S△COD=S△BOD,得出BD=CD=AC,进而得出BF=EF=OE=$\frac{1}{3}$n,再利用点C在反比例函数图象上得出点C坐标,最后利用点C在直线AB上即可求出n即可.
解答 解:①∵m+n=8,∴m=8-n,
∵点A(m,0),B(0,n)(m>0,n>0),
∴S△AOB=$\frac{1}{2}$n(8-n)=-$\frac{1}{2}$(n-4)2+8,
∴当n=4时,△AOB的面积最大,
②如图,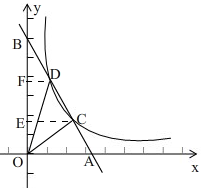
∵S△AOC=S△COD=S△BOD,
∴BD=CD=AC,
过点C作CE⊥OB于E,过点D作DF⊥OB于F,
∴DF∥CE∥OA,
∴BF=EF=OE,
∵点B(0,n)(n>0),
∴OB=n,
∴BF=EF=OE=$\frac{1}{3}$n,
∴点C的纵坐标为$\frac{1}{3}$n,
∵点C在反比例函数y=$\frac{m}{x}$(x>0)的图象上,
∴C($\frac{3m}{n}$,$\frac{1}{3}$n),
∵点A(m,0),B(0,n)(m>0,n>0),
∴直线AB的解析式为y=-$\frac{n}{m}$x+n,
∵点C在直线AB上,
∴-$\frac{n}{m}×\frac{3m}{n}+n=\frac{1}{3}n$,
∴n=$\frac{9}{2}$,
∴B(0,$\frac{9}{2}$).
点评 此题是反比例函数综合题,主要考查了三角形的面积公式,知识拓展得出的结论,待定系数法,解①的关键是建立三角形AOB的面积和n的函数关系式,解②的关键是得出BF=EF=OE=$\frac{1}{3}$n.


科目:初中数学 来源: 题型:解答题
 如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?
如图所示,小月家有四边形的田地ACBD,测量得∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=80cm,求这块菜地的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com