
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO�� 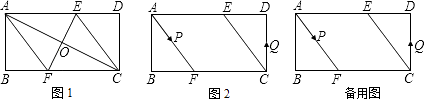
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У� ����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��
���𰸡�
��1���⣺�١��ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı��Σ�
�֡�EF��AC��
���ı���AFCEΪ���Σ�
�������εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ�����42+��8��x��2=x2��
���x=5��
��AF=5cm
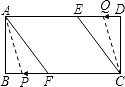
��2���⣺����Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P����AB��ʱ��Q����DE��CE�ϻ�P��BF��Q��CDʱ������ƽ���ı��Σ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=CD+AD��4t=12��4t����QA=12��4t��
��5t=12��4t��
��� ![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ�� ![]() �룮
�룮
��������ã��ı���APCQ��ƽ���ı���ʱ����P��Q�ڻ���ƽ�еĶ�Ӧ���ϣ�
�����������
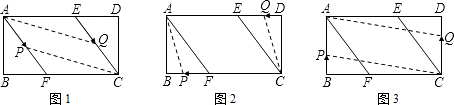
i����ͼ1����P����AF�ϡ�Q����CE��ʱ��AP=CQ����a=12��b����a+b=12��
ii����ͼ2����P����BF�ϡ�Q����DE��ʱ��AQ=CP����12��b=a����a+b=12��
iii����ͼ3����P����AB�ϡ�Q����CD��ʱ��AP=CQ����12��a=b����a+b=12��
����������a��b�����������ϵʽ��a+b=12��ab��0��
����������1����֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж������ݹ��ɶ����������AF�ij�����2���ٷ�������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ��ڷ�����������ۿ�֪a��b�����������ϵʽ��
�����㾫����������Ҫ�������߶δ�ֱƽ���ߵ����ʺ��ɶ����ĸ�������֪ʶ�㣬��Ҫ���մ�ֱ��һ���߶β���ƽ�������߶ε�ֱ���������߶εĴ�ֱƽ���ߣ��߶δ�ֱƽ���ߵ����ʶ������߶δ�ֱƽ�����ϵĵ�������߶������˵�ľ�����ȣ�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧΪ��սʡ�˻ᣬ��У�˶��ӵ�ѧ���н�����ȫ��ѡ�ֵ�ѡ�Σ������μ�ѡ��ѧ�����ۺϳɼ��ֳ����飬����������в�������ͳ��ͼ����
��� | �ɼ� | ����ֵ | Ƶ�� |
��һ�� | 90��x��100 | 95 | 4 |
�ڶ��� | 80��x��90 | 85 | m |
������ | 70��x��80 | 75 | n |
������ | 60��x��70 | 65 | 21 |
����ͼ����Ϣ���ش��������⣺
��1���μӻѡ�ε�ѧ�������ˣ�����m= �� n=��
��2���������������ֵ��Ϊ�����ƽ��ֵ���������μ�ѡ��ѧ����ƽ���ɼ���
��3������һ���е�4��ѧ����ΪA��B��C��D��������4��ѧ���������ۺ�ˮƽ�����־��������ѡ��������ѧ������ѧУ��������ͨ��������ͼ���б��ķ�����ǡ��ѡ��A��B�ĸ��ʣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ĵ�����װ��4���ʵء���С����ͬ��С����ЩС��ֱ��������3��4��5��x���ס�������ÿ��ͬʱ�Ӵ��и��������1����������������2��С��������֮�ͣ���¼��С��Żش��н��ȣ������ظ����飮ʵ���������±���
�����ܴ��� | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
����Ϊ8�����ֵ�Ƶ�� | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
����Ϊ8�����ֵ�Ƶ�� | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
����������⣺
��1�����ʵ�����������ȥ�������ϱ����ݣ����֡���Ϊ8����Ƶ�ʽ��ȶ������ĸ��ʸ��������Ƴ��֡���Ϊ8���ĸ�������
��2����x=7ʱ�������б�������״ͼ�����㡰��Ϊ8���ĸ��ʣ����ж�x=7�Ƿ���ܣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���̻�У����У������һ�鳤���β�ƺ����![]() �ף���
�ף���![]() �ף����ڲ�ƺ������ͼ��ʾ��ʮ��·����С·�Ŀ�Ϊ
�ף����ڲ�ƺ������ͼ��ʾ��ʮ��·����С·�Ŀ�Ϊ![]() �ף�
�ף�

![]() �ú�
�ú�![]() ��ʽ�ӷֱ��ʾ����ƺ�������С·�������
��ʽ�ӷֱ��ʾ����ƺ�������С·�������
![]() �
д��![]() �ж���ʽ�����������˵���Ǽ��μ���ʽ��
�ж���ʽ�����������˵���Ǽ��μ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90����ADƽ����CAB��DE��AB��E����AC=6��BC=8��CD=3��

��1����DE�ij���
��2������ADB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=��C=36�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�H��AC�Ĵ�ֱƽ���߽�BC�ڵ�E����AC�ڵ�G������AD��AE�������н��۴�����ǣ� �� 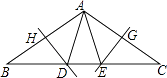
A.![]() =
= ![]()
B.AD��AE����BAC���ȷ�
C.��ABE�ա�ACD
D.S��ADH=S��CEG
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F��
��1����֤��EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ﵥ����ѧ����������һ��·ʱ������Ҫ��ij���飬�������ۻص��վ�����ij��꣬��������ȥѧУ����������������ѧ���õ�ʱ����·�̵Ĺ�ϵʾ��ͼ��
����ͼ���ṩ����Ϣ�ش��������⣺
��1��С���ҵ�ѧУ��·���Ƕ����ף�
��2����������ѧ��;���ĸ�ʱ���С���ﳵ�ٶ���죬�����ٶ��Ƕ�����/�֣�
��3��С�������ͣ���˶��ٷ��ӣ�
��4��������ѧ;�У�С��һ����ʻ�˶����ף�һ�����˶��ٷ��ӣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DΪBC�е㣬�ı���ABDE��ƽ���ı��Σ�AC��DE�ཻ�ڵ�O��
��1����֤���ı���ADCE�Ǿ��Σ�
��2������AOE=60�㣬AE=4�������ADCE�Խ��ߵij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com