
【题目】已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若方程有一个实数根为1,求m的值和另一个根.
【答案】(1)m≥![]() ;(2)m的值为1, 另一根为3
;(2)m的值为1, 另一根为3
【解析】
(1)由方程有两个实数根结合根的判别式△≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(2 )设x1为方程x2﹣2(m+1)x+m2+2=0的另一个根,根据根与系数的关系可得出x1+1=2(m+1),1×x1=m2+2,解方程组即可得出结论.
(1)∵关于x的方程x2﹣2(m+1)x+m2+2=0总有两个实数根,∴△=[﹣2(m+1)]2﹣4(m2+2)=8m﹣4≥0,解得:m≥![]() .
.
(2)∵x1为方程x2﹣2(m+1)x+m2+2=0的另一个根,∴x1+1=2(m+1),1×x1=m2+2.
解得:m=1,x1=3,∴m的值为1,另一个根为3.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
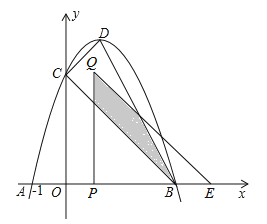
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角坐标系中,点![]() 分别在
分别在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .以
.以![]() 为边在第一象限作等边
为边在第一象限作等边![]() 垂直平分
垂直平分![]() .
.
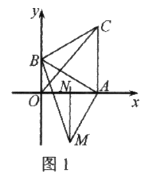
(1)求![]() 的长.
的长.
(2)求证:![]() .
.
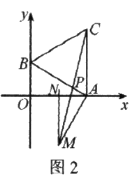
(3)如图2,连接![]() 交
交![]() 于点
于点![]() .点
.点![]() 是否为MC的中点?请说明理由.
是否为MC的中点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
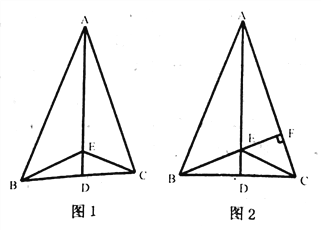
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45![]() ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小慧去某风景区游览,两人在景点古刹处碰面,相约一起去游览景点飞瀑,小聪骑自行车先行出发,小慧乘电动车出发,途径草甸游玩后,再乘电动车去飞瀑,结果两人同时到达飞瀑.图中线段![]() 和折线
和折线![]() 表示小聪、小慧离古刹的路程
表示小聪、小慧离古刹的路程![]() (米)与小聪的骑行时间
(米)与小聪的骑行时间![]() (分)的函数关系的图象,根据图中所给信息,解答下列问题:
(分)的函数关系的图象,根据图中所给信息,解答下列问题:
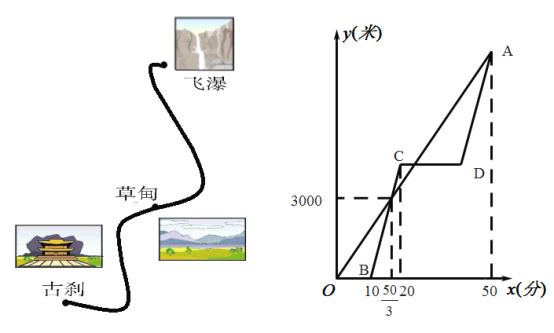
(1)小聪的速度是多少米/分?从古刹到飞瀑的路程是多少米?
(2)当小慧第一次与小聪相遇时,小慧离草甸还有多少米?
(3)在电动车行驶速度不变的条件下,求小慧在草甸游玩的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小志要到延庆冬奥综合训练馆参加滑冰训练,他们约定从德胜门出发自驾前往,但他们在选择路线时产生了分歧.根据导航提示小明选择方案1前往,小志选择方案2前往,由于方案1比方案2的路线长,而小明还想大家一起到达.已知小明的平均车速比小志的平均车速每小时快8千米,请你帮助小明算一算,他的平均车速为每小时多少千米,他们就可以同时到达?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com