
已知:关于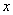 的一元二次方程
的一元二次方程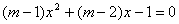 (m为实数)
(m为实数)
(1)若方程有两个不相等的实数根,求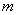 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论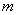 取何值,抛物线
取何值,抛物线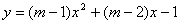 总过
总过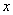 轴上的一个固定点;
轴上的一个固定点;
(3)若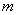 是整数,且关于
是整数,且关于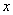 的一元二次方程
的一元二次方程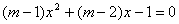 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线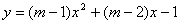 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
如图,已知一次函数y1=kx+b的图像与x轴相交于点A,与反比例函数y2=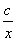 的图像相交于B(-1,5)、C(
的图像相交于B(-1,5)、C(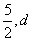 )两点.
)两点.
(1)求k、b的值;
(2)点P(m,n)是一次函数y1=kx+b的图像上的动点.
写出当-1<m≤2时,n的取值范围;
‚设m=1-a,如果在两个实数m与n之间(不包括m和n)有且只有一个整数,求实数a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,点A、B、C的坐标分别为(2,0),(3,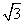 ),(1,
),(1,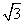 ),点D、E的坐标分别为(m,
),点D、E的坐标分别为(m,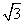 m),(n,
m),(n,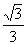 n)(m、n为非负数),则CE+DE+DB的最小值是 .
n)(m、n为非负数),则CE+DE+DB的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3,4三个数中任取的一个数,b是从l,2,3,4,5四个数中任取的一个数。定义“点M(a,b)在直线x+y=n上”为事件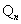 (2≤n≤9,n为整数),则当
(2≤n≤9,n为整数),则当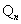 的概率最大时,n的所有可能的值为( )
的概率最大时,n的所有可能的值为( )
A.5 B.4或5 C.5或6 D.6或7
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数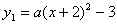 与
与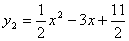 的图像的一个交点为
的图像的一个交点为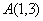 ,过点
,过点 作
作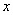 轴的平行线,分别交两条抛物线于点
轴的平行线,分别交两条抛物线于点 ,
,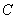 (点
(点 在点
在点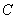 的左侧) .则下列结论:(1)无论
的左侧) .则下列结论:(1)无论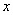 取何值,
取何值, 的值总是正数;(2)当
的值总是正数;(2)当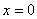 时,
时,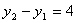 ;(3)当
;(3)当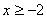 时,
时,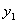 、
、 都随
都随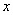 的增大而增大;(4)
的增大而增大;(4)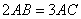 ;其中正确的是()
;其中正确的是()
A. (1) (2) B. (2) (3) C. (1) (3) (4) D. (1) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知平面直角坐标系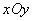 中的点
中的点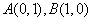 ,
,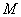 、
、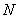 为线段
为线段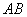 上两动点,过点
上两动点,过点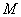 作
作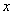 轴的平行线交
轴的平行线交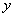 轴于点
轴于点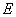 ,过点
,过点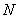 作
作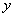 轴的平行线交
轴的平行线交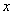 轴于点
轴于点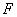 ,交直线
,交直线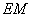 于点
于点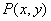 ,且
,且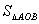 =
=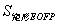 .
.
(1)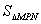
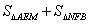 (填“>”、“=”、“<”),
(填“>”、“=”、“<”),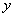 与
与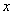 的函数关系是 (不要求写自变量的取值范围);
的函数关系是 (不要求写自变量的取值范围);
(2)当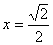 时,求
时,求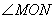 的度数;
的度数;
(3)证明: 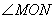 的度数为定值.
的度数为定值.
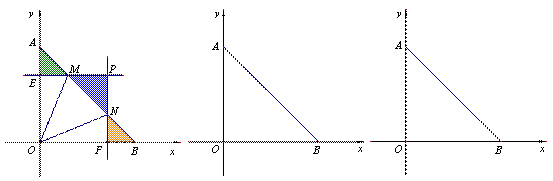
( 备用图) (备用图)
| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com