
【题目】如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1) (﹣2x)3﹣(﹣x)·(3x)2
(2) (2a+b)(4a2+b2)(2a﹣b)
(3)(π﹣3.14)0+(﹣1)3+(![]() )-3÷(﹣2)
)-3÷(﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2001年至2012年杭州市小学学校数量(单位:所)和在校学生人数(单位:人)的两幅统计图.由图得出如下四个结论: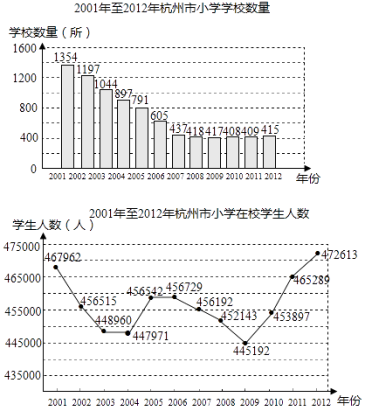
①学校数量2007年~2012年比2001~2006年更稳定;
②在校学生人数有两次连续下降,两次连续增长的变化过程;
③2009年的 ![]() 大于1000;
大于1000;
④2009~2012年,相邻两年的学校数量增长和在校学生人数增长最快的都是2011~2012年.
其中,正确的结论是( )
A.①②③④
B.①②③
C.①②
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,设x轴为直线l,函数y=﹣ ![]() x,y=
x,y= ![]() x的图象分别是直线l1 , l2 , 圆P(以点P为圆心,1为半径)与直线l,l1 , l2中的两条相切.例如(
x的图象分别是直线l1 , l2 , 圆P(以点P为圆心,1为半径)与直线l,l1 , l2中的两条相切.例如( ![]() ,1)是其中一个圆P的圆心坐标.
,1)是其中一个圆P的圆心坐标. 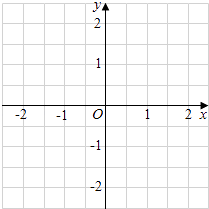
(1)写出其余满足条件的圆P的圆心坐标;
(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线lAC:y=﹣![]() 交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
交x轴、y轴分别为A、C两点,直线BC⊥AC交x轴于点B.
(1)求点B的坐标及直线BC的解析式;
(2)将△OBC关于BC边翻折,得到△O′BC,过点O′作直线O′E垂直x轴于点E,F是y轴上一点,P是直线O′E上任意一点,P、Q两点关于x轴对称,当|PA﹣PC|最大时,请求出QF+![]() FC的最小值;
FC的最小值;
(3)若M是直线O′E上一点,且QM=3![]() ,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
,在(2)的条件下,在平面直角坐标系中,是否存在点N,使得以Q、F、M、N四点为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作CDEF.
(1)当0<m<8时,求CE的长(用含m的代数式表示);
(2)当m=3时,是否存在点D,使CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得CDEF为矩形,请求出所有满足条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离y(m)与时间x(s)的函数关系图象是( )
A.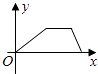
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com