
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A��6��0����B��0��8������C������Ϊ��0��m��������C��CE��AB�ڵ�E����DΪx���ϵ�һ���㣬����CD��DE����CD��DEΪ����CDEF��
��1����0��m��8ʱ����CE�ij����ú�m�Ĵ���ʽ��ʾ����
��2����m=3ʱ���Ƿ���ڵ�D��ʹCDEF�Ķ���Fǡ������y���ϣ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
��3����D�������˶������У�������Ψһ��λ�ã�ʹ��CDEFΪ���Σ��������������������m��ֵ��
���𰸡�
��1��
�⣺��A��6��0����B��0��8����
��OA=6��OB=8��
��AB=10��
�ߡ�CEB=��AOB=90�㣬
�֡ߡ�OBA=��EBC��
���BCE�ס�BAO��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��CE= ![]() ��
�� ![]() m
m
��2��
�⣺��m=3��
��BC=8��m=5��CE= ![]() ��
�� ![]() m=3��
m=3��
��BE=4��
��AE=AB��BE=6��
�ߵ�F����y���ϣ���ͼ2����

��DE��BO��
���EDA�ס�BOA��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
��OD= ![]() ��
��
���D�������� ![]() ��0��
��0��
��3��
�⣺ȡCE���е�P����P��PG��y���ڵ�G��
��CP= ![]() CE=
CE= ![]() ��
�� ![]() m��
m��
����m��0ʱ��
�ٵ�0��m��8ʱ����ͼ3����֤��GCP=��BAO��
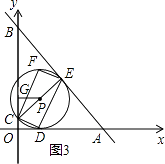
��cos��GCP=cos��BAO= ![]() ��
��
��CG=CPcos��GCP= ![]() ��
�� ![]() ��
�� ![]() m��=
m��= ![]() ��
�� ![]() m��
m��
��OG=OC+CG=m+ ![]() ��
�� ![]() m=
m= ![]() m+
m+ ![]() ��
��
��������ã��ã�OG=CP��
�� ![]() m+
m+ ![]() =
= ![]() ��
�� ![]() m��
m��
��ã�m= ![]() ��
��
�ڵ�m��8ʱ��OG��CP����Ȼ����������������m��ֵ��
����m=0ʱ������C��ԭ��O�غϣ���ͼ4����
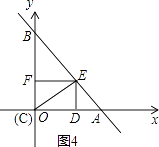
����m��0ʱ��
�ٵ���E���A�غ�ʱ������ͼ5����
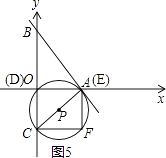
��֤��COA�ס�AOB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��ã�m=�� ![]() ��
��
�ڵ���E���A���غ�ʱ������ͼ6����
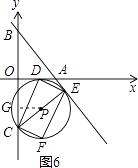
OG=OC��CG=��m���� ![]() ��
�� ![]() m��
m��
=�� ![]() m��
m�� ![]() ��
��
������ã�OG=CP��
�ੁ ![]() m��
m�� ![]() =
= ![]() ��
�� ![]() m��
m��
���m=�� ![]() ��
��
����������m��ֵ�� ![]() ��0��
��0�� ![]() ��
�� ![]() ��
��
����������1������֤����BCE�ס�BAO���������������εĶ�Ӧ�ߵı���ȼ�����ã���2��֤����EDA�ס�BOA���������������εĶ�Ӧ�ߵı���ȼ�����ã���3����m��0��m=0��m��0��������������ۣ���m=0ʱ��һ����������m��0ʱ����0��m��8��m��8����������������Ǻ����Ķ��弴����⣮��m��0ʱ���ֵ�E���A�غϺ͵�E���A���غ�ʱ����������������ۣ�


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y=��x+4����ֱ��l��ȡ��B1����B1�ֱ���x�ᣬy�������ߣ���x����A1����y����C1��ʹ�ı���OA1B1C1Ϊ�����Σ���ֱ��l��ȡ��B2����B2�ֱ���x�ᣬA1B1�����ߣ���x����A2����A1B1��C2��ʹ�ı���A1A2B2C2Ϊ�����Σ����˷�����ֱ��l��˳��ȡ��B3��B4������Bn��������������A2A3B3C3��A3A4B4C4������An��1AnBnCn����A3������Ϊ___��B5������Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Բ����������������Ⱥ��Բ��ƣ��ĸ�Ϊ12cm�������ܳ�Ϊ10cm���������ڱ��������ײ�3cm�ĵ�B����һ��������ʱһֻ����������������ڣ�������������3cm�ĵ�A���������ϳԵ����������е����·���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����֪y= ![]() ��x��0��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q����AQ��ȡAQ���е�ΪC��
��x��0��ͼ����һ��P��PA��x���ڵ�A��a��0������B����Ϊ��0��b����b��0��������M��y����������B���Ϸ��ĵ㣬����N������AP�ϣ�����B��AB�Ĵ��ߣ�������AP�ڵ�D����ֱ��MN�ڵ�Q����AQ��ȡAQ���е�ΪC��
��1����ͼ2������BP�����PAB�������
��2������Q���߶�BD��ʱ�����ı���BQNC�����Σ����Ϊ2 ![]() �����ʱP������ꣻ
�����ʱP������ꣻ
��3������Q������BD��ʱ����a=3��b=1�����Ե�B��C��N��QΪ������ı�����ƽ���ı��Σ������ƽ���ı��ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=a��x��1��2+4��x�ύ�ڵ�A��B����y�ύ�ڵ�C������C��CD��x�ύ�����ߵĶԳ����ڵ�D������BD����֪��A������Ϊ����1��0�� 
��1����������ߵĽ���ʽ��
��2��������COBD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪ����ԭ�㣬�ı���OABCΪ���Σ�A��10��0����C��0��8������P�ڱ�BC����ÿ��1����λ�����ٶ��ɵ�C���B�˶���ͬʱ��Q�ڱ�AB����ÿ��a����λ�����ٶ��ɵ�A���B�˶����˶�ʱ��Ϊt�루t��0����
��1��������������y= ![]() ͼ��P�㡢Q�㣬��a��ֵ��
ͼ��P�㡢Q�㣬��a��ֵ��
��2����OQ��ֱƽ��AP����a��ֵ��
��3����Q���˶���AB�е�ʱ���Ƿ����aʹ��OPQΪֱ�������Σ������ڣ����a��ֵ������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ��һ���ı��εĿյ�ABCD����ͼ��ʾ��Ϊ���̻�������ѧУ�ƻ��ڿյ�����ֲ��Ƥ����������A=90�㣬AB=3m��DA=4m��BC=12m��CD=13m��
��1������յ�ABCD�������
��2����ÿ��ֲ1ƽ���ײ�Ƥ��Ҫ200Ԫ�����ܹ���Ͷ�����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ�����λͬѧ�ڲٳ��ϻ��ഫ����������䴫���ǵȿ��ܵģ������ɼ����ȿ�ʼ����
��1������2�δ�������Իص������еĸ�������
��2�������оٷ�������״ͼ���б�����3�δ�������Իص������еĸ��ʣ�
��3�����벢ֱ��д�����ۣ�����n�δ�������ס�������λͬѧ���еĸ��ʣ�P���������У���P���������У��Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���

��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM����BOC���ڲ�����ǡ��ƽ����BOC���ʣ���ʱֱ��ON�Ƿ�ƽ����AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��6�����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ�������AOC����t��ֵΪ ��ֱ��д���������
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON����AOC���ڲ�������AOM����NOC�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com