
判断关于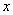 的方程
的方程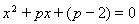 的根的情况.
的根的情况.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2012届江苏省高邮市九年级上学期期中考试数学试卷(带解析) 题型:解答题
课堂上对关于x的方程: 的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
(1)请找一个m的值代入方程使方程的两个根为互不相等的整数,并求这两个根;
(2)请选择乙或丙同学的发现加以判断,并说明理由。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年初中数学湘教版九年级上册第1章练习卷(解析版) 题型:解答题
已知关于 的方程
的方程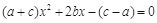 的两根之和为
的两根之和为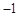 ,两根之差为1,其中
,两根之差为1,其中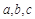 是△
是△ 的三边长.
的三边长.
(1)求方程的根;(2)试判断△ 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省高邮市九年级上学期期中考试数学试卷(解析版) 题型:解答题
课堂上对关于x的方程: 的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
(1)请找一个m的值代入方程使方程的两个根为互不相等的整数,并求这两个根;
(2)请选择乙或丙同学的发现加以判断,并说明理由。
查看答案和解析>>
科目:初中数学 来源:《第2章 一元二次方程》2010年创新题(解析版) 题型:解答题
 .
. 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.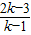 =0,解得k=
=0,解得k= .
. 是
是 =0的解.
=0的解. 时,方程的两实数根x1,x2互为相反数.
时,方程的两实数根x1,x2互为相反数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com